Pole obszarow plaskich Kasia: Witam, czy moglabym poprosic o pomoc w rozwiazaniu nastepujacego zadania: Oblicz pole obszarow plaskich ograniczonych krzywymi: y=sin2x , y=sinx , 0≤x≤π Pole ma byc rowne 4 π, prosze o jakakolwiek pomoc w rozwiazaniu tego zadania, Dziekuje

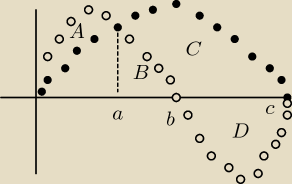
AS: o o o y = sin(2*x) czarne kropki y = sin(x) Ustalam punkt przecięcia krzywych sin(2*x) = sin(x) 2*sin(x)*cos(x) − sin(x) = 0 sin(x)*(2*cos(x) − 1) = 0 sin(x) = 0 lub cos(x) = 1/2 → x = 0 lub x = π (c) lub x = π/3 (a)

	−1
Całka podstawowa: ∫sin(a*x)dx =		*cos(a*x)
	a

Pole obszaru A π/3 π/3 P1 = ∫(sin2x − sinx)dx = (−1/2)*cos2x + cosx| = (−1/2)*(−1/2) + 1/2 − (−1/2 + 1) = 0 0 = 1/4 + 1/2 + 1/2 − 1 = 1/4 Pole obszrau B π/2 π/2 P2 = ∫sin2xdx = −cos2x | = −(−1/2) − 0 = 1/2 π/3 π/3 Pole obszaru C π π P3 = ∫sinxdx = −cosx| = −(−1) + 1/2 = 3/2 π/3 π/3 Pole obszaru D π π P4 = |∫sin2xdx| = |−1/2*cos2x| | = |−1/2*1 + 1/2*(−1)| = −1/2 − 1/2| = |−1| = 1 π/2 π/2 Pole szukane

	1
P = P1 + P3 − P2 + P4 = 1/4 + 3/2 − 1/2 + 1 = 2
	4