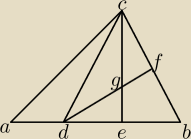
 zad.1
Punkty D, E dzielą bok ABC trójkąta na trzy odcinki mające taką samą długość. Punkt F jest
środkiem boku BC. Odcinki CE i DF przecinają się w punkcie G. Oblicz stosunek pola trójkąta
CDG do pola trójkąta ABC.
zad.1
Punkty D, E dzielą bok ABC trójkąta na trzy odcinki mające taką samą długość. Punkt F jest
środkiem boku BC. Odcinki CE i DF przecinają się w punkcie G. Oblicz stosunek pola trójkąta
CDG do pola trójkąta ABC.

| 2 | ||
Wyszło mi | . Dobrze? | |
| 9 |

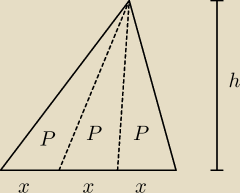
| 1 | ||
Po pierwsze ... zauważ, że trójkąty Δacd, Δcde i Δceb mają takie samo pole (i wynosi | ||
| 3 |
| 1 | ||
Ponadto można zauważyć, że PΔfdc = PΔfdb ( i każde z nich wynosi | pola ΔABC) | |
| 3 |
