optymalizacja Mathamaniac: Ostrosłupy, których podstawą są prostokąty o stosunku długości boków 1:2, umieszczamy w kuli o promieniu √3 w taki sposób, że wierzchołek każdego ostrosłupa jest środkiem kuli, a wszystkie wierzchołki podstawy należą do powierzchni kuli. Jaką maksymalną objętość może mieć tak umieszczony w kuli ostrosłup?

Jerzy: I gdzie masz problem ?

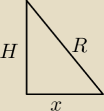
Jerzy: 1) wysokość bryły H ( wykorzystujesz fakt,że krawędź boczna jest promieniem kuli) 2) wzór na objetość ostrosłupa ( funkcja dwóch krawędzi podstawy ) 3) eliminacja jednej zmiennej (ze zwiazku pomiedzy krawedziami podstawy) 4) maksimum funkcji jednej zmiennej

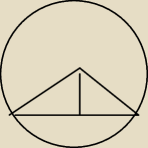
Mathamaniac: No i podstawa tego trójkąta to jakieś 5x, przeciwprostokątna √3

Mathamaniac: h=√3−25x²/4

Mathamaniac: V=2x²*h

Mathamaniac: No i razy 1/3

Mathamaniac: Czy to jest ok?

Jerzy:

	√a2 + b2
x=
	2

Jerzy: W powyższym wzorze: a i b to krawędzie podstawy , i dodatkowo: a = 2b

Mathamaniac: Już zrobione.