Geometria analityczna
Pati18773: Okrąg O
1 o środku w punkcie (4,−2) jest styczny do osi OX. Okrąg ten przekształcono przez
| | 3 | |
jednokładność w skali k=− |
| i środku w punkcie P należącym do prostej x+2y=0. W ten |
| | 2 | |
sposób otrzymano okrąg O
2. Podaj równanie okręgu O
2 jeśli:
a) jest on styczny do osi OX
b) jest styczny do osi OY
20 mar 21:44
adam: a) (x + 6)2 + (y − 3)2 = 9
21 mar 13:26
Jerzy:
Mam pytanie, czy promień okręgu zmienia się w skali jednokładności ?
21 mar 13:39
adam: Tak.
21 mar 14:38
Pati18773: A można wiedzieć jak to wyszło ?
21 mar 19:08
adam: Współrzędne środka okręgu O1 mnożysz przez k, czyli −3/2, i masz środek okręgu O2,
a promień okręgu O1 mnożysz przez |k|, bo promień nie może być ujemny, i masz promień O2.
Okrąg O1 jest styczny do OX, więc jego promień to |y|, czyli 2.
21 mar 20:15
adam: Ogólnie przy jednokładności:
współrzędne mnożysz przez k,
długości przez |k|,
pole przez k2
Gdy k jest ujemne, to elementy figury przekształconej znajdą się po drugiej stronie punktu
(0,0).
21 mar 20:22
Pati18773: w odpowiedzi są po dwa rozwiązania, jak wyznaczyć promień okręgu O1 ?
22 mar 17:16
Pati18773: dobra chyba już wiem Xd
22 mar 17:21
Pati18773: wyszła mi odp (x+6)2+(y−2)2=9
nie wiem skąd jest (x−6)2+(y+2)2=9
22 mar 17:29
Pati18773: widzę to na rysunku ale nie wiem jak zapisać to aby mi to drugie równanie wyszło
22 mar 18:07
Pati18773: nikt nie naprowadzi ?
22 mar 19:32
adam: Zaraz, zaraz
! Jeśli okrąg O
1 ma środek (4,−2) i jest styczny do OX, to nie może być
równocześnie styczny do OY.
Więc i okrąg O
2 nie może być styczny do OY.
Chyba że w zadaniu jest mowa też i o innym okręgu, np. jakiś O
1 bis, który jest styczny do OY.
22 mar 20:01
Pati18773:
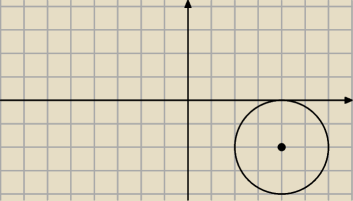
okrąg O
1 wygląda tak wiec jak może być styczny do OY
22 mar 20:07
adam: No sama widzisz, że nie może.
Poza tym prawidłowa odpowiedź to
(x + 6)2 + (y − 3)2 = 9
22 mar 20:10
Pati18773:
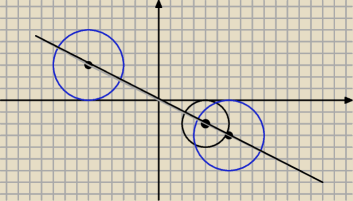
w odpowiedzi są dwa równania i wygląda to tak
22 mar 20:15
Pati18773: no i jeden okrąg jest znaleziony ale jak ten drugi o środku (6;−3)
22 mar 20:19
adam: Ten okrąg pod osią OX jest dla k=3/2 (bez znaku minus), bo znajduje się po tej samej stronie
punktu (0,0) co okrąg O1.
22 mar 20:21
Pati18773: ale k jest z minusem
22 mar 20:33
Pati18773: ale k jest z minusem
22 mar 20:34
adam: Więc cóż... Ja upieram się przy swoim, autor podręcznika przy swoim. Sama musisz zdecydować,
kogo posłuchasz.
22 mar 20:45