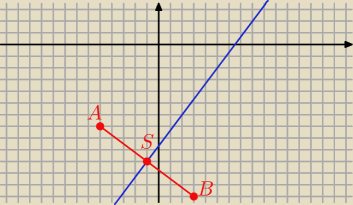
ostatki cynamonek: dany jest odcinek o końcach A = (−5,−7) B = (3, − 13) wyznacz rówanie w którje zawarta jest symetralna tego odc. S = ( −1, −10 ) obliaczam prostą (y+7)(3 + 5) − (−13 +7) (x+5) = 0 y − 3/4 x − 43/4 prostopadła a = 4/3 − 10 = 4/3 *−1 + c c = −26/3= − 8 i 2/3 y = − 4/3x − 8 i 2/3

Janek191:

	− 13 −(−7)		− 6		3
a =		=		= −
	3 − (−5)		8		4

Prosta prostopadła

	4
y =		x + b
	3

	4
− 10 =		*(−1) + b
	3

	4
− 10 +		= b
	3

	26
b = −
	3

	4		26
y =		x −
	3		3

====================

cynamonek: dzięki zrobiłem też dobrze ale inną metodą ale w porządku znać inne

Janek191: Jak dobrze, gdy zły wynik ?

Mila: II spsób: A = (−5,−7) B = (3, − 13) Symetralna odcinka jest zbiorem wszystkich punktów płaszczyzny jednakowo odległych od końców tego odcinka. P(x,y) − dowolny punkt symetralnej AB √(x+5)²+(y+7)²=√(x−3)²+(y+13)²⇔ (x+5)²+(y+7)²=(x−3)²+(y+13)² 4x−3y−26=0

	4		26
y=		x−
	3		3