ojj cynamonek: Podstawa AB trójkąta równoramiennego ABC, w którym |AC|=|BC| jest zawarta w prostej o równaniu y=⁴₃x +6. Wyznacz współrzędne wierzchołka B, jeśli wiadomo, że A=(−3,2) C = (4,7) Wyliczam prostą AC (y−2)(4+3) − (7−2) (x+3) = 0 y = ⁵₇ x + ²⁹₇ teraz wyznaczam prostą CB. AC i BC są prostopadłe to wyliczam współczynik a a = − ⁷₅ cb −−−> y= − ⁷₅ x + c podstawiam współrzędne wierzchołka C 7 = − ⁷₅ * 4 + c c = ⁶³₅ y_cb = − ⁷₅ + ⁶³₅ i równanie prostej CB oraz AB − ⁷₅ x + ⁶³₅ = ⁴₃ x + 6 i reszte juz obliczam

Jerzy: A dlaczego uważasz,że proste AC i BC są prostopadłe ?

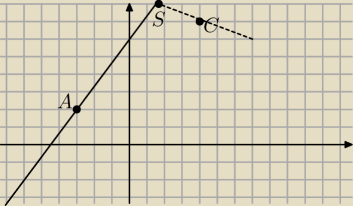
Antonni: w zwaizku z tym ze masz trojkat rownoramienny to mozesz zrobic tak

	4
1 napisac rownaie prostej prostopadlej do		x+6 i przechodzacej przez C
	3

2. Policzyc punkt przeciecia sie obu prostych Masz wtedy wspolrzedne S srodka odcinka BA Ze wzorow na srodek odcinka liczysz wpolrzedne punktu B

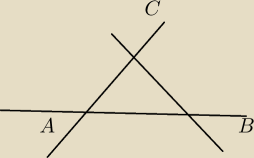
cynamonek: Ponieważ jeśli są to proste i są wierzchołkiem w tym trójkącie to się przetną. Czy źle myślę ?

Jerzy: Przetną, ale niekoniecznie pod kątem prostym Zrób tak, jak napisał Antonni.

cynamonek: y = 4/3x +6 to prosto prostopadła y = −3/4 x + 10 układ równań i mi wychodzą pkt ( 48/25 ; 36/25 ) a jeśli podłożę to do X_b + 4 / 2 = 48/25 to wychodzą mi jakieś absurdy tak samo z Y_b. Chyba ,że coś źle robię

adam: Albo: wyznaczasz odległość r=AC i z układu równań: {prostej AB {okręgu o środku S=C i promieniu r=AC wyznaczasz B. B=(171/25,378/25)

cynamonek: to zadanie rozwiązane mam na 4 sposoby i każdy wynik inny Mila gdzie jesteś ?

Mila: Przygotowuję kolację , a o co chodzi? Wpisz pytanie, abym nie musiała wszystkiego czytać/

cynamonek: Podstawa AB trójkąta równoramiennego ABC, w którym |AC|=|BC| jest zawarta w prostej o równaniu y=43x +6. Wyznacz współrzędne wierzchołka B, jeśli wiadomo, że A=(−3,2) C = (4,7) Jaka czujna

adam: cynamonek: zdecyduj się, czy równanie to: y=43x +6 czy y=4/3x +6 jak to napisałeś w pierwszym poście.

cynamonek: tak jak w pierwszym y=4/3x +6 − PRZEPRASZAM! zjadło mi ;C

cynamonek: to chyba przez to, że mila kolację robi i zgłodniałem

adam: No bo jakbym nie zauważył twojej pomyłki, to Mila dałaby ci piąty wynik.

cynamonek: dzięki adam Dobrze,że mamy tutaj takich czujnych ludzi

Mila: Liczę, cierpliwości Panowie.

Mila:

	4
y=		x+6
	3

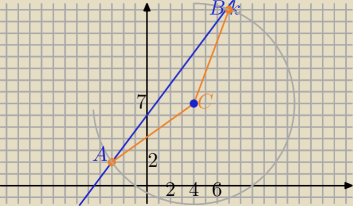
A=(−3,2) ,C = (4,7) |AC|=|BC| |AC|=√7²+5²=√74 Teraz geometryczna konstrukcja (kreślę okrąg o środku w punkcie C i R=|AC|. ) Szukam punktu przecięcia z prostą AB co algebraicznie opiszemy tak:

	4
(x−4)2+(y−7)2=74 i y=		x+6
	3

x=−3 i y=2 to punkt A

	171		378
x=		i y=		to
	25		25

	171		378
B=(		,		)
	25		25

To wynik Adama.

cynamonek: Dziękuję Wybacz Adam za moją niewierność , Lubię być pewny

adam: Spoko, sam często się mylę.

cynamonek: Tak patrzę, patrzę i nie widzę > w miejsce y podstawiam tą prostą tak? Bo tak coś drogi do rozwiązania odnaleźć nie mogę

Mila:

	4
(x−4)2+(		x+6−7)2=74
	3

	16		8
x2−8x+16+		x2−		x+1=74
	9		3

25		32
	x2−		x−57=0
9		3

licz dalej sam

adam: Tak

cynamonek: dzięki