Funkcja wykładnicza Targon: Wyznacz wszystkie wartości parametru m, dla których równanie 2 ^x+2 ^x−1+2 ^x−2+...=2 ^2x−1+m ma jedno rozwiązanie. Wychodzi mi że m∊(−∞, 0)u({2} a w odpowiedziach przy 0 jest domkniete

Tadeusz: to 2^2x−1 na pewno jest za znakiem =

Targon: Tak

Jerzy: Jaką masz lewą stronę równania ?

Tadeusz:

	1
po lewej masz zatem ciąg w którym a1=2x q=
	2

Targon: Dałem że 2^x=a suma po lewej wyszła 2. To mam 2a=(a²/2)+m

Targon: I tutaj liczyłem jedno ze Δ=0 i t>0 a drugie że Δ>0 i t1t2<0

Jerzy: No to zła suma Ci wyszła.

Targon: Czemu zła

Jerzy: Dobra ... już widzę:

	t2
Masz równanie: 2t =		+ m .
	2

Jakie nałożyłeś/ aś warunki ?

Targon: No napisałem je wyżej

Targon: I tutaj liczyłem jedno ze Δ=0 i t>0 a drugie że Δ>0 i t1t2<0

Jerzy: Masz dobry wynik: m ∊ (−∞;0) U {2}

karty do gry: A co jeśli t₁ * t₂ = 0 ? Wtedy jeden z nich będzie zerem a drugi ?

Targon: W odpowiedziach jest zamknięty przy 0

Targon: Może ma być ze t1t2≤0

Jerzy: Racja ....dla m = 0 mamy t₁ = 0 lub t₂ = 4.

Targon: Czyli mam dodać założenie czy zmienić?

Jerzy: Nakładasz dwa warunki: 1) t₁*t₂ ≤ 0 2) t₁ + t₂ > 0

Targon: No tak ale w tym 3 ²x−2(m−1)3^x +m+5=0 gdzie też ma jedno rozwiazanie to brałem te założenia co podałem wyżej I mi wyszło

Jerzy: Przypadek , bo w tym równaniu dla m = 0 mamy brak rozwiazań.

Targon: W tym drugim jak przyjmę te twoje założenia to nie mam wgl części wspólnej więc nie mogę ich wziąć

Targon: Ktoś pisał że Domknięcie nie wynika z założeń (kwadratowe); tylko z tego, że suma po lewej może być równa pierwszemu składnikowi prawej dla jednego x−sa.

Targon: Tu chyba musi być jakis warunek dlatego że po lewej mamy szereg bo w zadaniach bez szeregów normalnie wychodzi

Jerzy: Co rozumiesz pod pojęciem: "nie mam wgl części wspólnej" ?

Targon: No zrób drugie równanie dla twoich założeń i zobaczysz że nic Ci nie wyjdzie

Jerzy: Jeśli rozpatrujesz dwa odzielne przypadki: 1) Δ = 0 lub 2) Δ > 0 , to nie interesuje Cie część wspólna, bo to jest alternatywa ( czyli suma ).

Targon: Chodzi mi o drugi przypadek z Δ>0 że dla twoich założeń nic nie wyjdzie

Jerzy: 1) m ∊ (−∞;− 1) U ( 4;+∞) 2) m ≤ − 5 3) m > 1 i co , twierdzisz nadal, że nie ma części wspólnej ?

Targon: No ja zaznaczam na osi te 3 przypadki i żadne 3 się że sobą nie pokrywają

Jerzy: Przemyj oczy ,narysuj oś liczbową i popatrz jeszcze raz.

Targon: No zaznaczam 3 przypadki na różnych wysokościach i nigdzie 3 mi się razem nie pokrywają

Targon: Mam 3 przypadki i w żadnym miejscu na osi te 3 się nie spotkają

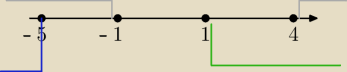
Jerzy: Nadal nie widzisz części wspólnej ?

Targon: Zielony i niebieski nie nadchodzą na siebie

Jerzy: Teraz to ja idę przemyć oczy wodą

Targon: A zakładając że masz rację to i tak w odpowiedziach przy − 5 jest otwarte a nie zamknięte

Targon: Dlatego nie rozumiem czemu w tym przypadku będzie klasycznie Δ>0 i t1t2<0 a w przypadku z szeregiem trzeba co innego

Jerzy: Dla : Δ > 0 mamy: [t₁*t₂ ≤ 0 i t₁ + t₂ > 0] ⇔ \ [t₁*t₂ = 0 i t₁ + t₂ > 0 lub t₁*t₁ < 0 i t₁ + t₂ > 0 czyli mamy alternatywę. (A U B) ∩ C ⇔ A ∩ C lub B ∩ C

Jerzy: I teraz sprawdź, który przypadek zachodzi w tym przykładzie.

Targon: W tym zajdzie tylko gdy Δ>0 i t1t2<0

Targon: Gdzie indziej ludzie pisali ze Domknięcie wynika z tego że mamy szereg

Jerzy: Nie ma to znaczenia.

Targon: To już nie rozumiem. Skąd mam wiedzieć jakiego założenia użyć. Zadania maja tą samą treść a trzeba inne założenia

Jerzy: W obydwu zadaniach założenia są identyczne. A) Δ = 0 i x_w > 0 ( jeden pierwiastek dodatni ( B) Δ > 0 1) t₁*t₂ ≤ 0 ( dwa różnych znaków lub jeden równy zero ) 2) t₁ + t₂ > 0 ( gdy jeden równy zero, to drugi dodatni)

Targon: Jak w drugim przykładzie dasz t1t2≤0 i t1+t2>0 to wyjdzie zła odpowiedź

Targon: Tym bardziej że sam napisałeś że z tych przedziałów nie zrobisz części wspólnej

Jerzy: Jeszce raz ....t₁*t₂ ≤ 0 i t₁ + t₂ > 0 ⇔ (t₁*t₂ = 0 i t₁ + t₂ > 0 ) lub (t₁*t₂ < 0 i t₁ + t₂ > 0)

Jerzy: Teraz mamy alternatywę ( sumę przedziałów )

Targon: I wychodzi mi inna odpowiedź niż w odpowiedziach

Jerzy: A jaka jest odpowiedź do drugiego przykładu ?

Targon: Normalnie jak widzę w internecie to ludzie mówią że funkcja ma jedno rozwiazanie gdy Δ=0 i t>0 lub Δ>0 i t1t2<0.Te założenia w pierwszym przykładzie nie dają poprawnej odpowiedzi natomiast w drugim już jest poprawna

Targon: m∊(−∞, 5)u{4}.4 wyjdzie z Δ=0 i t>0

Targon: A przedział (−∞, − 5) z Δ>0 i t1t2<0

Jerzy: Samo założenie Δ > 0 i t₁*t₂ < 0 wyklucza przypadek, w którym jeden pierwiastek jest równy 0 , a drugi dodatni ( nie mozemy go pominąć )

Jerzy: Pytam o końcową odpowiedź do zadania, a nie o jakieś Twoje przemyslenia.

Targon: To jest końcowe z końca książki

Targon: m∊(−∞, − 5)u{4}

Targon: Na innych stronach każdy pisał że Δ>0 i t1t2<0 i tutaj się sprawdza natomiast w pierwszym już nie

Jerzy: OK. W takim razie w podobnych przypadkach, czyli takich, gdzie wyraz wolny c trójmianu ax² + bx + c , jest zależny od parametru ( tutaj c = m + 5 ), sprawdzaj, czy dla c = 0 drugi pierwiastek jest dodatni ( ponieważ dla c= 0 , trojmian ma zawsze jeden pierwiastek: x = 0 )

Targon: Czyli muszę dać Δ>0 i t1t2<0 i sprawdzać c gdy c jest zależne od m?

Jerzy: Tak. Musisz sprawdzić, czy przy c = 0 drugi pierwiastek jest dodatni, czy ujemny.

Targon: Ok dzięki wielki. Nie za trudne to na poziom rozszerzony? Na maturze nigdy bym nie wpadł żeby sprawdzić C