 Dla jakiej wartosci parametru a zbior rozwiazan nierownosci
x2−3x+2<0
jest zawarty w zbiorze rozwiazan nierownosci
ax2−(3a+1)x+3>0
Rozwiazuje nierownosc x2−3x+2<0
Δ=1 x1= 1 x2= 2
x∊(1,2)
Dla a=0 dostaje nierownosc stopnia pierwszego
−x+3>0
−x>−3
x<3 czyli x∊(−∞.3)
Dla a=0 zbior rozwiazan nierownosci x2−3x+2 jest zawarty w zbiorze rozwiazan nierownosci
ax2−(3a+1)x+3>0
Teraz gdy a≠0
Wiec wyroznik trojmianu ax2−(3a+1)x+3 wynosi
Δ= [−(3a+1)]2−4*a*3= 9a2+6a+1−12a= 9a2−6a+1= (3a−1)2
√(3a−1)2= |3a−1|
Wedlug mnie teraz musimy rozpatrzec trzy przypadki
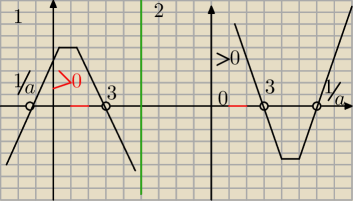
1. dla a<0 |3a−1|= 1−3a
Dla jakiej wartosci parametru a zbior rozwiazan nierownosci
x2−3x+2<0
jest zawarty w zbiorze rozwiazan nierownosci
ax2−(3a+1)x+3>0
Rozwiazuje nierownosc x2−3x+2<0
Δ=1 x1= 1 x2= 2
x∊(1,2)
Dla a=0 dostaje nierownosc stopnia pierwszego
−x+3>0
−x>−3
x<3 czyli x∊(−∞.3)
Dla a=0 zbior rozwiazan nierownosci x2−3x+2 jest zawarty w zbiorze rozwiazan nierownosci
ax2−(3a+1)x+3>0
Teraz gdy a≠0
Wiec wyroznik trojmianu ax2−(3a+1)x+3 wynosi
Δ= [−(3a+1)]2−4*a*3= 9a2+6a+1−12a= 9a2−6a+1= (3a−1)2
√(3a−1)2= |3a−1|
Wedlug mnie teraz musimy rozpatrzec trzy przypadki
1. dla a<0 |3a−1|= 1−3a
| 1 | ||
2. dla a∊(0, | ) |3a−1|= 1−3a | |
| 3 |
| 1 | ||
3. dla a∊< | ,∞) |3a−1|= 3a−1 | |
| 3 |
| 3a+1−(1−3a) | ||
x1= | = 3 | |
| 2a |
| 3a+1+1−3a | 1 | |||
x2= | = | |||
| 2a | a |
| 1 | ||
ale a<0 wiec | <0 | |
| a |
| 1 | |
>3 | |
| a |
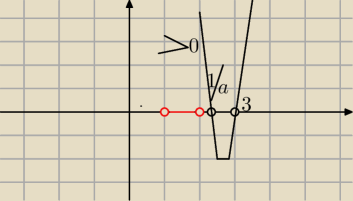 nr 3
Dla tego przypadku
nr 3
Dla tego przypadku
| 3a+1−(3a−1) | 1 | |||
x1= | = | |||
| 2a | a |
| 3a+1+3a−1 | ||
x2= | = 3 | |
| 2a |
| 1 | 1 | 1 | ||||
x∊(1,2) bedzie sie zawieral w x∊(−∞, | ) gdy | ≥2 to a≤ | ||||
| a | a | 2 |
| 1 | 1 | |||
Po uwzgledniemiu ze a≥ | mamy ze a∊<U{1}{3. | > | ||
| 3 | 2 |
| 1 | ||
Odp do wszystkich przypadkow to a∊(−∞, | > | |
| 2 |
 Bylo to zadanie maturalne na ocene celujaca wiec myslalem ze tak wlasnie nalezy .
Bylo to zadanie maturalne na ocene celujaca wiec myslalem ze tak wlasnie nalezy .