Trójkąty podobne
Cezary:
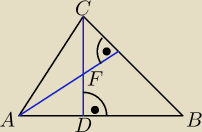
Trójkąt o bokach różnej długości zamieszczony na rysunku obok, zawiera trójkąty, które nie są
podobne. Te trójkąty to:
A. ΔADF i ΔCEF
B. ΔADC i ΔACE
C. ΔABE i ΔBCD
D. ΔADF i ΔBCD
Czy pomoże mi ktoś zrobić to zadanie i wytłumaczyć? Nic tak nie ogarniam z matmy jak właśnie
tego podobieństwa trójkątów...
19 mar 20:18
kochanus_niepospolitus:
gdzie jest punkt E ?
19 mar 20:25
Cezary: Zapomniałem zaznaczyć, przy drugim kącie prostym.
19 mar 20:33
Cezary:
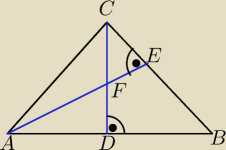
19 mar 20:35
Janek191:
Odp. C
19 mar 20:37
Janek191:
Źle. Raczej B)
19 mar 20:40
Cezary: Ale wie ktoś dlaczego B?
W odpowiedziach sprawdziłem − tak B.
19 mar 20:48
Tadeusz:
raczej A

19 mar 20:54
Tadeusz:
błąd ... przepraszam
19 mar 20:56
kochanus_niepospolitus:
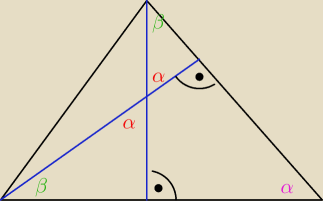
To dlaczego oba kąty czerwone są sobie równe chyba nie muszę wyjaśniać (jest to klucz do
rozwiązania zadania)
a) skoro mamy w obu trójkątak po kącie prostym i po kącie α, to brakujący kąt będzie taki sam
(i niech wynosi on β)
c) w wierzchołku B będziemy mieli kąt α (bo wcześniej ustaliliśmy, że α+β = 90
o)
d) także są podobne bo mają takie same kąty
więc drogą eliminacji wychodzi odp. B (ponieważ ΔADC nie ma kątów α i β
19 mar 20:56
kochanus_niepospolitus:
(b) mogłoby być prawdą jedynie gdyby 2β = α ... czyli α = 60o ; β = 30o ... ale wtedy ΔABC
były równoboczny ... a to jest sprzeczne z danymi z zadania
19 mar 20:58
Cezary: Dzięki kochanus
niepospolitus

19 mar 21:06
 Trójkąt o bokach różnej długości zamieszczony na rysunku obok, zawiera trójkąty, które nie są
podobne. Te trójkąty to:
A. ΔADF i ΔCEF
B. ΔADC i ΔACE
C. ΔABE i ΔBCD
D. ΔADF i ΔBCD
Czy pomoże mi ktoś zrobić to zadanie i wytłumaczyć? Nic tak nie ogarniam z matmy jak właśnie
tego podobieństwa trójkątów...
Trójkąt o bokach różnej długości zamieszczony na rysunku obok, zawiera trójkąty, które nie są
podobne. Te trójkąty to:
A. ΔADF i ΔCEF
B. ΔADC i ΔACE
C. ΔABE i ΔBCD
D. ΔADF i ΔBCD
Czy pomoże mi ktoś zrobić to zadanie i wytłumaczyć? Nic tak nie ogarniam z matmy jak właśnie
tego podobieństwa trójkątów...


 To dlaczego oba kąty czerwone są sobie równe chyba nie muszę wyjaśniać (jest to klucz do
rozwiązania zadania)
a) skoro mamy w obu trójkątak po kącie prostym i po kącie α, to brakujący kąt będzie taki sam
(i niech wynosi on β)
c) w wierzchołku B będziemy mieli kąt α (bo wcześniej ustaliliśmy, że α+β = 90o)
d) także są podobne bo mają takie same kąty
więc drogą eliminacji wychodzi odp. B (ponieważ ΔADC nie ma kątów α i β
To dlaczego oba kąty czerwone są sobie równe chyba nie muszę wyjaśniać (jest to klucz do
rozwiązania zadania)
a) skoro mamy w obu trójkątak po kącie prostym i po kącie α, to brakujący kąt będzie taki sam
(i niech wynosi on β)
c) w wierzchołku B będziemy mieli kąt α (bo wcześniej ustaliliśmy, że α+β = 90o)
d) także są podobne bo mają takie same kąty
więc drogą eliminacji wychodzi odp. B (ponieważ ΔADC nie ma kątów α i β
