trojkat StrasznyNieogar: Podstawą trojkata rownoramiennego ABC jest odcinek o koncach A (2, 1) i B (5, 2). Jedno z ramion trojkata zawiera się w prostej 2x − y − 3 = 0. Oblicz współrzędne C. A więc robie tak: 1. Sprawdzam które ramię się zawiera w podanej prostej. Jest to ramię AC, bo B nie należy do tej prostej 2. Liczę D, czyli środek podstawy. Tam pada wysokość trojkata z wierzcholka C, bo jest rownoramienny. 3. Wyznaczam wzór prostej AB, a potem prostopadlej do niej, zawierającej punkt D. 4. Teraz wystarczy przecięcie obu prostych (punkt C) gdzie robie błąd? Bo nie wychodzi.

Antonni: pewnie w rachunkach

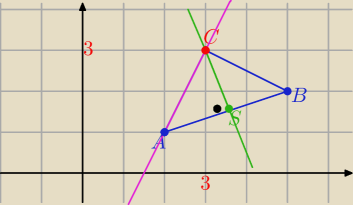
Eta: Do prostej y= 2x−3 należy punkt A

	7		3
Środek odcinka AB : S(		,		)
	2		2

	yB−yA		1
współczynnik kierunkowy prostej AB : aAB=		= ... =
	xB−xA		3

to współczynnik kierunkowy prostej SC ⊥AB : a_SC=−3 prosta SC: y=−3(x−x_S)+y_S ⇒ y=−3x+12 rozwiązując układ równań: y=2x−3 i y=−3x+12 otrzymujesz .... C(3,3)