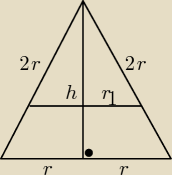
Przekrój osiowy stożka jest trójkątem równobocznym... bob: Przekrój osiowy stożka jest trójkątem równobocznym, a jego przekrój płaszczyzną równoległą do płaszczyzny podstawy ma pole równe 9π. Uzasadnij że objętość tego stożka jest większa od 48. Wykonaj rysunek pomocniczy i zaznacz na nim przekrój płaszczyzną równoległą do płaszczyzny podstawy.

bob: spróbuje ktoś?

bob:

Anna: pomogę

Anna: Pole przekroju poziomego : P = 9π V = ? πr₁² = 9π ⇒ r₁² = 9 ⇒ r₁ = 3

	2r√3
h =		= r√3
	2

	1
V =		πr2h
	3

	1		1
V =		πr2 * r√3 =		πr3√3
	3		3

	1
Gdyby r = r1 =3 , to : V =		π*27√3 ≈ 3,14 * 9 * 1,7 ≈ 48,042 > 48.
	3

A r > r₁, zatem objętość całego stożka tym bardziej jest większa od 48.

bob: dzięki za rozwiązanie a czy jest inny sposób na rozkminke tego zadania, np. z talesa? Bo gdyby r było mniejsze to ten sposób by nie wypalił