W trójkącie równoramiennym ABC podstawa AB zawiera się w prostej KACPER98PL: k: x−y−15=0, zaś ramię BC zawiera się w prostej l: x+2y−12=0. Punkt P(2;−1) należy do ramienia AC. Oblicz wysokość tego trójkąta poprowadzoną na podstawę AB.

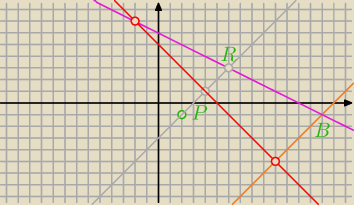
Tadeusz: Przez P prowadzimy równoległą do AB a dalej jak na rysunku

Tadeusz: dziękuję ci kacperku ... warto ci pomagać

KACPER98PL: Punkt P należy do ramienia AC, a nie lata gdzieś poza trójkątem. Tyle w temacie.

Tadeusz: ty głąbie .. lataj w temacie ... bo i tak g... z tego rozumiesz

KACPER98PL: Fak ju men!

Pytający:

KACPER98PL: Kto się może nazywać jak Tadeusz?

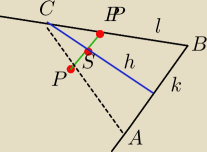
adam: równoległa do k przez P y = x − 3 P' na prostej l (6,3) środek S między PP' (4,1) prostopadła h do k przez S y = 5 − x wierzchołek C (−2,7) odległość C k 12√2 Odp. Wysokość h= 12√2

adam:

KACPER98PL: I o to mi chodziło! Dzięki