geometria analityczna Pati18773: Oblicz odległość środka okręgu x²−2x+y²−4y=0 od prostej y=−2x+9. Sprawdź ile punktów wspólnych mają okrąg i prosta. x²−2x+y²−4y=0 ⇒ (x−1)²+(y−2)²=6 S(1;2) r=√6 y=−2x+9 2x+y−9=0 odległość wyznaczyłam i wyszło √5 czyli tak jap powinno być mam problem z punktami wspólnymi w układzie równań zapisałam (x−1)²+(y−2)²=6 i y=−2x+9 podstawiłam za y (x−1)²+(−2x+9−2)²=6 (x−1)²+(7−2x)²=6 x²−2x+1+49−28x+4x²=6 5x²−30x+44=0 Δ=20 √Δ=2√5 wychodzą mi dwa rozwiązania a w odp jest jedno

Janek191: x² − 2 x + ( −2 x + 9)² − 4*( −2 x + 9) = 0 x²−2 x + 4 x² − 36 x + 81 + 8 x − 36 = 0 5 x² − 30 x + 45 = 0 / : 5 x² − 6 x + 9 = 0 ( x − 3)² = 0 x = 3 ==== y = 3 ====

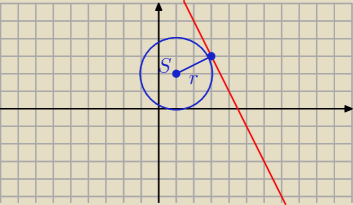
Janek191: S = ( 1, 2) r = √5

Pati18773: to trzeba tak oddzielnie podstawiać ?

Janek191: Źle wyliczyłaś promień okręgu.

Janek191: x² −2 x + y² − 4y = 0 ( x − 1)² − 1 + ( y − 2)² − 4 = 0 (x −1)² + ( y − 2)² = 5 r = √5

Pati18773: ahhh no tak .... dziękuję !