... brzoza: Dwa przystające okręgi:jeden o środku P=(4,5) ,drugi o środku Q=(8,9) są styczne zewnętrznie. Zapisz równanie osi symetrii figury złożonej z tych okręgów,nieprzechodzącej przez ich środki.

Jerzy: To prosta prostopadła do prostej AB przechodząca prze środek odcinka AB (symetralna odcinka AB)

Jerzy: Prostej PQ oczywiście.

kochanus_niepospolitus: oś symetrii będzie prostą przechodzącą przez środki tych dwóch okręgów druga oś symetrii może być prostopadła do wcześniejszej linii symetrii przechodząca przez punkt styczności okręgów (przy założeniu że oba okręgi posiadają taki sam promień )

Jerzy: Jeśli nie mają takiego samego promienia,to mają tylko jedną oś symetrii.

Janek191:

	4
a =		= 1
	4

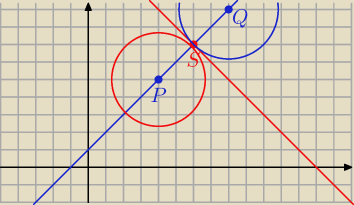
y = x + b P = ( 4, 5) 5 = 4 + b ⇒ b = 1 pr. P Q : y = x + 1 Prosta prostopadła przechodząca przez środek odcinka PG S = ( 6, 7) y = − x + k 7 = − 6 + k ⇒ k = 13 y = − x + 13 ==========

brzoza: czyli będzie miała odwrotny współczynnik kierunkowy co prosta przechodząca przez środki

	1
np. jeśli pierwsza ma a=2 to druga ma a=−
	2

Janek191: To przystające okręgi, więc r₁ = r₂ = r

brzoza: równanie 1 prostej (tej przechodzącej przez środki) y=x+1 a jak będzie wyglądać równanie tej drugiej?

Janek191: Patrz : 17.20

brzoza: bo mi wychodzi że y=−x+13 ale to chyba burak

brzoza: ale nie.... zgadza się

adam: Wyznaczasz środek odcinka PQ: S=(6, 7) Wyznaczasz równanie prostej przechodzącej przez PQ: y = x + 1 Wyznaczasz prostą prostopadłą przechodzącą przez S: y = − x + 13