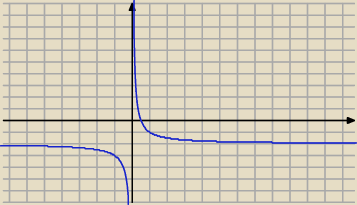
Przedziały wartosci dodatnich i ujemnych w funkcji homograficznej Agata4762: Mam pytanie co do funkcji homograficznej, dokładniej chodzi o przedziały w których funkcja ma wartości dodatnie i ujemne. 1 przykład: a>0, miejsce zerowe = 1/2, asymptota pionowa = 0 A więc f < 0 <===> x ∊ (−∞, 0) ∪ (1/2, +∞) f > 0 <===> x ∊ (−∞, 1/2) ∪ (0, +∞) 2 przykład: a<0, miejsce zerowe = 5/4, asymptota pionowa = 0 f < 0 <===> x ∊ ( −∞, 5/4) ∪ ( 0, +∞) f > 0 <===> x ∊ (−∞, 0) ∪ ( 5/4, +∞) Dobrze zapisałam te przedziały? Bo w 2 przykładzie inne rozwiązanie mam z lekcji a inne jest w odpowiedziach i w końcu nie wiem któro jest dobre. Ps. to co zapisałam jest z odpowiedzi, a w zeszycie mam odwrotnie

wredulus_pospolitus: warunek a>0 czy też a<0 to za mało ... masz podaną konkretną funkcję f(x) czy też nie?

wredulus_pospolitus: http://www.math.edu.pl/funkcja-homograficzna

Agata4762: Do 1 przykładu wzór to f(x) = 1/x − 2 , a dla drugiego f(x) = −5/x + 4

wredulus_pospolitus:

1		1
	czy		− 2
x−2		x

Agata4762: 1 − 5 − − 2 i − + 4 x x

wredulus_pospolitus:

1		1
	− 2 ... jest to zwykły wykres		i 'obniżony' o 2 w dół
x		x

	1
jak wygląda wykres f(x)=		chyba wiesz ... prawda
	x

w drugim przykładzie masz na odwrót przedziały ponieważ właśnie masz 'a' <0 (−5)

Agata4762: Czyli te przedziały mam dobrze zapisane?

Agata4762: Dziękuje !

Antonni:

	1
Wykres funkcji y=		−2
	x