Planimetria-matura podstawowa
Tomaszek: W trapezie ABCD o podstawach AB i CD dane są długości przekątnych |AC|=8 i |BD|=12 oraz Pola
PABG=18 i PCDG=2. Punkty E i F są środkami odpowiednio przekątnych BD i AC. Oblicz pole
trapezu ABEF.
G to punkt przecięcia przekątnych.
sprawdzi ktoś odpowiedź bo nie wiem czy mam dobrze PABEF=16
18 mar 15:17
Adamm:
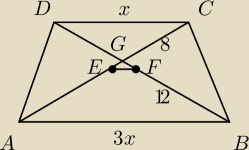
18=2*k
2 ⇒ k=3
|AG|=6, |BG|=9
|EG|=6−4=2
| | 2 | | 1 | |
stąd już wiadomo że trójkąt EFG jest podobny w skali |
| = |
| do ABG |
| | 6 | | 3 | |

18 mar 15:37
SPANKrock: Dlaczego AG = 6 ? mamy w poleceniu przecież tylko że AE= 4 skąd ta dwójka ?
14 maj 14:09
Eta:
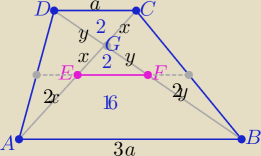
Z treści zadania:
ΔCDG≡ΔEFG to P(DCG)=P(EFG)=2
zatem P(ABFE)=P(ABG)−P(EFG) ⇒ P(ABFE)=18−2=
16 [j
2]
14 maj 15:42
 18=2*k2 ⇒ k=3
|AG|=6, |BG|=9
|EG|=6−4=2
18=2*k2 ⇒ k=3
|AG|=6, |BG|=9
|EG|=6−4=2

 Z treści zadania:
ΔCDG≡ΔEFG to P(DCG)=P(EFG)=2
zatem P(ABFE)=P(ABG)−P(EFG) ⇒ P(ABFE)=18−2=16 [j2]
Z treści zadania:
ΔCDG≡ΔEFG to P(DCG)=P(EFG)=2
zatem P(ABFE)=P(ABG)−P(EFG) ⇒ P(ABFE)=18−2=16 [j2]