stereometria Tomaszek: Podstawą ostrosłupa jest równoramienny trójkąt prostokątny ABC o przeciwprostokątnej AB. Wysokością ostrosłupa jest odcinek SS', gdzie S' jest środkiem okręgu opisanego na podstawie.Odległość punktu S' od krawędzi bocznej AS jest równa b, a kąt między krawędzią AS, a wysokością ostrosłupa ma miare α.Oblicz objętość ostrosłupa

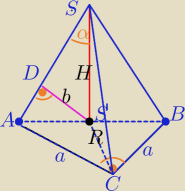
Mila: S' − środek okręgu opisanego na trójkącie ABC ( środek przeciwprostokątnej) |AS'|=R=|S'C| Poradzisz sobie teraz?

Tomaszek:

b		b
	=sinα ⇔ H=
H		sinα

R
	=tgα
H

R=Htgα

	b		sinα		b
R=		*		=
	sinα		cosα		cosα

	a√2
|AS'|=		=R
	2

a√2		b
	=
2		cosα

	√2b
a=
	cosα

	2b
a√2=
	cosα

	1		1		√2b		√2b		b
V=		*		*		*		*
	3		2		cosα		cosα		sinα

	1		2b3
V=		*
	6		cos2αsinα

dobrze

Mila: Dobrze. Mogłeś tak po obliczeniu R i H:

	1
PΔABC=		a2
	2

	1
(2R)2=a2+a2 stąd:		a2=R2
	2

	b2
PΔABC=R2=
	cos2α

	1		b2		b
V=		*		*
	3		cos2α		sinα