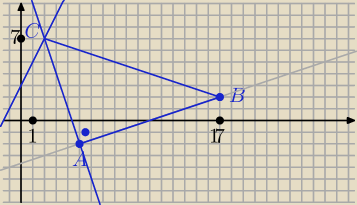
Geometria analityczna majsa: Punkty A=(5,−2) i B=(17,2) są wierzchołkami trójkąta prostokątnego ABC o kącie prostym przy wierzchołku A. Wierzchołek C należy do prostej o równaniu y=2x+3 A)wyznaczanie współrzędne wierzchołka C B) oblicz pole trójkąta ABC Proszę o dokładne rozwiązanie ,bo mi nie chce wyjść

Janek191:

	4		1
a =		=
	12		3

	1
y =		x + b A = ( 5, −2)
	3

	11
− 2 = U{5}[3} + b ⇒ b = −
	3

	1		11
y =		x −
	3		3

================== Prosta prostopadła y = −3 x + k A = ( 5, − 2) − 2 = −3*5 + k ⇒ k = 13 y = − 3 x + 13 ========== Punkt C −3 x + 13 = 2 x + 3 5 x = 10 x = 2 y = 2*2 + 3 = 7 C = (2, 7) ===========

Antonni: Panie Janku191 I to b musi byc ?

Janek191: ?

Janek191: B ) → AB = [ 12, 4] → AC = [ −3, 9 ] więc I AB I = √12² + 4² = √144 + 16 = √16*10 = 4√10 I AC I = √(−3)² + 9² = √ 9 + 81 = √9*10 = 3√10 Pole Δ ABC P= 0,5* 4 √10*3√10 = 6*10 = 60 ============================= II sposób P = 0,5 * I 12*9 − (−3)*4 I = 0,5* I108 + 12I = 60 =====================================

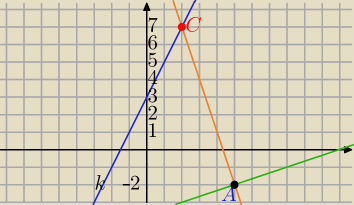
Mila: 1) k: y=2x+3 A=(5,−2) i B=(17,2) AB^→=[12,4] AC⊥AB Prosta AC: m: 12(x−5)+4*(y+2)=0 3x+y−13=0 Punkt przecięcia prostych k i m 3x+2x+3−13=0 5x=10 ⇔x=2 i y=2*2+3=7 C=(2,7) 2) AC^→=[−3,9]

	1
PΔ=		*|det M|
	2

M: 12 4 −3 9 Det(..)=12*9+12=120

	1
PΔABC=		*120=60
	2