Geo analityczna maska: Dany jest punkt A = (−1, 2) Wyznacz rownanie takiej prostej przechodzącej przez pubkt A, że odległość początku układu współrzędnych od tej prostej jest rowna 1. Ta prosta będzie miała jeden punkt wspólny z okregiem o promieniu 1 i środkiem w początku układu współrzędnych wzór x² + y² = 1 Nie wiem jak dalej pociągnąć to zadanie.

Jerzy: Z pęku prostych przechodzących przez A , wybierz tą, której odległość od zadanego punktu wynosi 1.

maska: Tzn jak? Bo takie proste mogą być dwie żeby były styczne z okregiem i przechodziły przez punkt

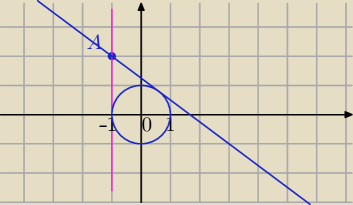
Mila: A = (−1, 2) y−2=m*(x+1) równanie prostej w postaci kierunkowej x=1 − jedna z prostych y−2=mx+m⇔ k: mx−y+2+m=0

	|m*0−0+2+m|
d((0,0),k)=		=1
	√m2+1

|2+m|=√m²+1 /² 4+4m+m²=m²+1 4m=−3

	3
m=−
	4

	3		3
k: y=−		x−		+2
	4		4

	3		5
y=−		x+
	4		4

========== II sposób Ax+By+C=0 −A+2B+C=0⇔C=A−2B Ax+By+A−2B=0

	|A*0+B*0+A−2B|
d((0,0),k)=		=1
	√A2+B2

|A−2B|=p{A²+B²| /² A²−4A*B+4B²=A²+B² −4A*B+3B²=0 B*(−4A+3B)=0 B=0 to mamy prostą Ax+0*y+A−2*0=0⇔Ax+A=0 ⇔x+1=0 lub 3B=4A

	3
A=		B
	4

3		3
	B*x+B*y+		B−2B=0
4		4

3		5
	x+y−		=0 /*4
4		4

3x+4y−5=0 ===============

maska: No tak... Dziękuję