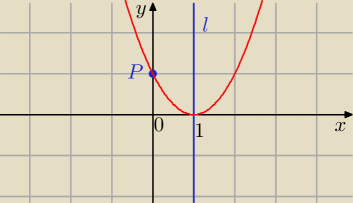
Zadanie (pełne) z funkcji kwadratowej Chalwa: Wykres funkcji f(x)=x² + bx + c jest symetryczny względem prostej l i przecina oś OY w punkcie P. Wyznacz współcznynnik f w postaci kanonicznej: l: x=1 P(0,1)

Antonni: Powiadasz wspolczynnik f?

Janek191: Mamy p = 1 f(0) = 1 więc f(x) = (x − 1)² + q 1 = 1 + q ⇒ q = 0 Odp. f(x) = ( x −1)² = x² − 2 x + 1 b = − 2 c = 1 ===================

Chalwa: Dobrze, ale jakim sposobem zamieniłeś (x−1)² na 1 ?

Janek191: Jakie 1 ?

Chalwa: Nie, spoko już nic.W tym równaniu (x−1)² za x podstawiłeś 0 w efekcie czego zostało samo ,,−1"² czyli 1. Sprostuj proszę jeśli się mylę, Dziękuję bardzo za pomoc

Janek191: a = 1 p = 1 W równaniu f(x) = (x −1)² + q za x podstawiłem 0 , a 1 za f(x) więc 1 = ( 0 − 1)² + q 1 = 1 + q q = 0 zatem f(x) = ( x −1)² + 0 = ( x −1)² = x² − 2 x + 1 a = 1 b = − 2 c = 1

Antonni: Tak Mozna to zadanie zrobic takze tak Z warunkow zadania wiemy ze a=1 b=? i c=1 bo P przecina os OY . A wspolczynnik c informuje nas o tym w jaka jest wspolrzedna y punktu przeciecia osi OY Wiemy ze prosta l na rownanie x=1 to oznacza ze x_w=p=1

	−b		−b
xw=		⇒1=		⇒b=−2
	2a		2

Postac ogolna tej funkcji jest taka y=x²−2x+1 to posatc kanoniczna y=(x−1)²