Udowodnić prawa de Morgana
Mn: Udowodnić prawa de Morgana
Jak to zrobić, np za pomocą tabelki, czy coś
16 mar 18:31
KKrzysiek: no to w algebrze bool'a
~(x+y) = ~X*~y
=(!x+!y)* (!x+y)*(x+!y)
= (!x+!yy)(x+!y)
=(!x+0)(x+!y)
=0+!x!y
=~x*~y
16 mar 19:17
Mn: no spoko, a te prawa de morgana to jest tylko 1?
16 mar 19:18
KKrzysiek: No są dwa, ale drugie sobie sam udowodnij, jedna podpowiedź : skorzystaj z twierdzenia o
idempotetności
16 mar 19:19
KKrzysiek: ~(x*y) = ~x+~y
=(~x*~y) + (~x*y) +(x*~y) wzór kanoniczny
=(~x*~y) + (~x*y) +(x*~y) * (~x*~y) z twierdzenia o idempotetności
16 mar 19:20
KKrzysiek: =...
16 mar 19:21
Mn: nie no ale jakaśtabelka 0 i 1 , wpisać tylko wartośći,
bo jest tylko kilka przypadków
16 mar 20:17
KKrzysiek: TO JEST TABLICA PRAWDY, a nie dowód
16 mar 20:23
Mn: ale tak magister udowodnił u nas z architektury komputerów
16 mar 21:22
KKrzysiek: eh.. może to nie był dowód?
pokaż zdjęcie , że tak było, bo nie uwierzę
16 mar 21:23
Mn: nie no, takie było polecenie, nie. udowdnij.
myślisz że ja notuje 0o
tabelką, bo powiedział że każdy matematyk uzna dowód bo to jest tabelka, tak
ale w niej są wszystkie przypadki, na internecie chyba też takie widziałem
16 mar 21:27
KKrzysiek: No to podeślij, bo dla mnie to nie dowód
16 mar 21:27
Mn: oczywiśćie chodzi tutaj, o bramki logiczne itp.
nie wiem ja się nie znam, mam to dziadostwo elektroniczne, i musze umieć
16 mar 21:27
KKrzysiek: Jaki byłby sens pokazywania prawa de morgana w postaci tablicy prawdy? Co chciał wam w ten
sposób przekazać? Może chodziło tylko o pokazanie przekształcenia bramek logicznych do bramek
NAND lub NOR używając prawa de morgana. NIe będę się domyślał, podeślij więcej informacji, bo
dyskusja nie ma sens. Inaczej, ja nie rozumiem jak to można tabelką udowodnić. Pewnie da się
to rozłożyć na czynniki i przedstawić w postaci tabelki, ale dalej nie widzę sensu takiego
pomysłu.
16 mar 21:30
16 mar 21:30
Mn: no i co ?
16 mar 21:33
KKrzysiek: No dobra... rachunkiem zdań... u mnie takich dowodów się nie przeprowadza.
16 mar 21:33
KKrzysiek: Zrobienie takiej tabelki jest proste, robisz w ten sposób:
16 mar 21:33
Adamm: dowód polega na wykazaniu że (p ⋀ q)' ⇔ p' ∨ q' oraz że (p ∨ q)' ⇔ p' ∧ q'
tabelką można wykazać że jest to tautologia
16 mar 21:34
KKrzysiek: !(p ⋀ q) <=> !p v !q
Masz 2 zmienne: p i q i 4 przypadki
p q
0 0
0 1
1 0
11
staraj się wpierw otrzymać koniunkcję p i q, a następnie w osobnej kolumnie otrzymać negacje
tej koniunkcji, tak jest najprościej, czyli
p ⋀ q
0
0
0
1
!(p ⋀ q)
1
1
1
0
−−−−
!p v !q
−wpierw liczysz negację dla atomu p i osobno negację dla atomu q
później składasz w całość i liczysz alternatywę tych dwóch zdań
to w sumie wszystko
16 mar 21:37
Mn: dobra spoczko, umiem hyba, umiecie możę Zaimplementować następującą funkcję logiczną
(narysować schemat logiczny):
wykorzystując tylko bramki NAND. Założyć, że są dostępne zarówno zmienne, jak również
ich negacje. − > coś takiego, ew. gdzie znależć informacje na ten temat, jakieś sensowne
16 mar 21:37
KKrzysiek: dowód powinien tak wyglądać:
(p ⋀ q)' ⇔ p' ∨ q'
x ∉ p ⋀ q <=> x ∉p v x ∉ q <=> !(x ∊ p ) v !(x ∊ q) <=> x ∊ !p v x ∊ !q <=> x ∊ !p v !q
16 mar 21:39
KKrzysiek: Nie wiem gdzie takowe informacje możesz znaleźć, ale zauważ , że bramkę NOT możesz narysować
jako bramkę NAND wtw. gdy masz zwarte wejścia.
Bramkę AND bodajże jako dwie bramki NAND
nor jako 3 , a or jako 4.
To znaczy, rozrysuje sobie , lub zaneguj dwa razy funkcję logiczną, i będziesz widział ile
bramek NAND musisz narysować.
16 mar 21:41
Mn: no nie wiem jak się to robi, no nie wiem o co ci chodzi
16 mar 21:51
16 mar 21:56
KKrzysiek: powiem inaczej, nie będę streszczał Ci tutaj godzinnego wykładu z elektroniki
16 mar 21:56
Mn: no dzięki ci, ale
będzie tam odp jak za pomocą zmienić na bramki nor mor itd.?
16 mar 22:02
Mn: ej czekaj co to za syf, tutaj nic nie jest wyjaścione, a jak klikam na rozwiązanie to mi pisze
jakieś l
iczby a chodziło mi o funkcje i zapisanie ich za pomocą bramek
16 mar 22:05
16 mar 22:06
16 mar 22:14
KKrzysiek: Nie musi.
16 mar 22:15
Mn: a co musze
16 mar 22:42
KKrzysiek: Nic nie musisz
17 mar 12:02
Mn: wiem o tym, a co musze aby umiec
17 mar 12:55
17 mar 13:51
17 mar 14:05
Aby umieć, nauczyć musisz się.
https://en.wikipedia.org/wiki/NAND_logic
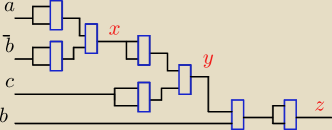
Rozrysowałem Ci połowę zadania (niebieskie prostokąty to bramki NAND):
_
x=a+b
_
y=(a+b)+c=a+b+c
_
z=(a+b+c)*b
