Przekątne trapezu ABCD przecinają się w punkcie P. KACPER98PL: Prosta równoległa do podstaw trapezu przechodząca przez punkt P, przecina ramiona AD i BC odpowiednia w punktach M i N. Wykaż, że |MP|=|NP|

Mila:

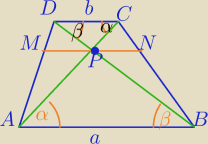
	b		|CP|		b		b
ΔDCP∼ΔABP w skali k=		⇔		=		⇔|CP|=		*|AP|
	a		|AP|		a		a

MP||DC⇔ΔAPM∼ΔADC

|MP|		|DC|		|MP|		b
	=		⇔		=		⇔
|AP|		|AC|		|AP|		|AP|+|CP|

|MP|		|AP|
	=		⇔
b		b   |AP|+ *|AP|   a

|MP|		1
	=		⇔
b		b   1+   a

|MP|		a
	=
b		a+b

	a*b
|MP|=
	a+b

analogicznie |

	a*b
|NP|=		⇔
	a+b

|MP|=|NP| =======

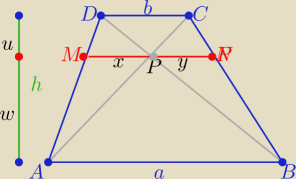Eta: Inny sposób: |MP|=x , |NP|=y , x,y>0 mamy wykazać,że x=y Z podobieństwa trójkątów ABD i MPD oraz ABC i NPC z cechy (kkk)

a		w+u		a		w+u		a		a
	=		oraz		=		to		=		⇒ x=y
x		u		y		u		x		y

c.n.w