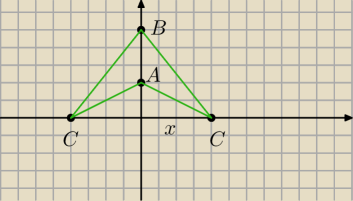
trójkąt Cezary: Dane są punkty A = (0,2) i B = (0,5). Wyznacz współrzędne punktu C wiedząc że leży on na osi Ox a trójkąt abc ma pole równe 3.

Jerzy:

	1		1
P(ABC) =		x*5 −		x*2 ... i oblicz : x
	2		2

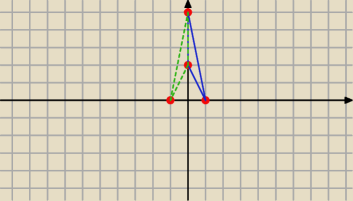
Adamm: C=(x₀;0) u=C−A=<x₀;−2> v=C−B=<x₀;−5> u•u=x₀²+4 v•v=x₀²+25 v•u=x₀²+10

	x02+4 x02+10 x02+10 x02+25
P=(		)1/2=3|x0|

skoro pole ma być równe 3 to mamy x₀=1 lub x₀=−1

Jerzy: Adamm , Twój trójkąt ABC ma pole: P = 1, 5

Adamm: właśnie wiem, muszę poszukać ten wzór na pole jeszcze raz

Jerzy:

	1
3 =		(5x − 2x) ⇔ 6 = 3x ⇔ x = 2
	2

Szukane punkty: C = (2:0) lub C(−2;0)

Cezary: x = 2 lub x = −2 mi wyszło jak podstawiłem od Ciebie Jerzy, a wynik ma być jakimś cudem C (6,0) lub C(−6,0)

Jerzy: Połowa modułu iloczynu wektorowego AB^→ x AC^→

Jerzy: A łyżka na to: "niemożliwe".

Cezary: Czyli błąd w odpowiedziach?

Adamm:

	1		x02+4 x02+10 x02+10 x02+25		3
wiem czemu, P=		(		)1/2=		|x0|
	2				2

skąd x₀=2 lub x₀=−2

	1
zapomniałem o		z przodu
	2

Jerzy: A no właśnie .... połowa równoległoboku rozpietego na wektorach: AB i AC

Jerzy: Cezary .... tak, to błąd w odpowiedzi.

Cezary: Jeszcze pytanie Jerzy, dlaczego w tym wzorze odejmujesz większą wysokość (większe pole) czyli Od B do C od tej mniejszej (od A do C) Czyli 5 i 2.

Jerzy: P(ΔABC) = P(Δ0BC) − P(Δ0AC) ... popatrz na rysunek.

Cezary: OK, dzięki.