stereometria Tomaszek: Dany jest ostrosłup prawidłowy czworokątny, którego podstawa ABCD jest kwadratem o boku 6. Odległość spodka wysokości ostrosłupa od krawędzi bocznej jest równa 4. Wyznacz objętość ostrosłupa i cosinus kąta między kolejnymi scianami bocznymi tego ostrosłupa. Objętość obliczyłem V=144 , ale nie wiem gdzie znajduje się ten kąt.

Jerzy: Przetnij go płaszczyzną przechodzącą przez przekatną podstawy i prostopadłą do jego krawędzi.

Tomaszek:

	−1		1
wyszło mi		a powinno −
	17		5

Tomaszek: wiem, że trzeba zastosować twierdzenie cosinusów (6√2)²=h²+h²−2h²cosa

Tomaszek: obliczyłem wysokość ściany bocznej z twierdzenia pitagorasa 12²+3²=h² 144+9=h² h²=153 h=3√17

	1		1
P=		*a*h=		*6*3√17=9√17
	2		2

potem policzyłem znowu tw. pit i obliczyłem krawedz boczna b=9√2

1
	*9√2*H=9√17
2

√2H=2√17 H=√34 i co mam źle

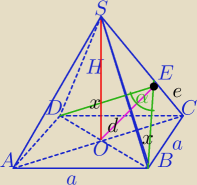
Mila: a=4,d=4

	1
1) |OC|=		*6√2=3√2
	2

e=√2

d		H		4		H
	=		⇔		=
e		|OC|		√2		3√2

H=12

	1
V=		*62*12=144
	3

−−−−−−−−−−−−−− 2) W ΔEOB: x²=(3√2)²+4²=18+16=34 W ΔDBE: |DB|²=x²+x²−2*x*x*cos α (6√2)²=34+34−2*34*cosα 72=68−68cosα 4=−68 cos α

	1
cosα=−
	17