Dla jakich wartości parametru m równanie ma cztery różne rozwiązania?
Tomasz: Witam,
Potrzebuję pomocy z zadaniem.
Dla jakich wartości parametru m równanie x2+2(m−3)|x|+m2−1=0 ma cztery różne rozwiązania?
Zabrałem się za to rozpatrując dwa przypadki, w pierwszym x<0, a w drugim x≥0. Następnie
sprawdziłem dla jakiej wartości parametru m delta jest większa od zero. Jednak w obu
przypadkach wyszedł mi taki sam przedział m<−4/3. Czy to jest dobrze? Niestety nie mam
odpowiedzi do tego zadania.
15 mar 22:51
Pytający:
Dwa układy:
dla x≥0 oba miejsca zerowe muszą być nieujemne:
Δ>0
x
1x
2≥0
x
1+x
2≥0
dla x<0 oba miejsca zerowe muszą być ujemne:
Δ>0
x
1x
2>0
x
1+x
2<0
Rozwiązanie to część wspólna obu rozwiązań.
A co do delty:
| | 5 | |
Δ=(±2(m−3))2−4(m2−1)=4m2−24m+36−4m2+4=40−24m>0 ⇔ m< |
| . |
| | 3 | |
15 mar 23:38
Tomasz: Nie za bardzo rozumiem skąd wzięły się warunki, że x1x2>0 i x1+x2>0
15 mar 23:43
Janek191:
Jeżeli x1 i x2 mają być nieujemne, to x1 + x2 ≥ 0 i x1*x2 ≥ 0
15 mar 23:50
Tadeusz:
nie musisz rozpatrywać dwóch przedziałów .... a dlaczego ... odpowiedz sobie sam
15 mar 23:56
Janek191:
x2 = I x I2
15 mar 23:58
Tadeusz:
a w sumie f(|x|) ... i wniosek
16 mar 00:03
Tomasz: Hmm... A dlaczego przyjmujemy że miejsca zerowe mają być nieujemne/większe od 0?
16 mar 00:17
Tadeusz:
odpowiedz sobie na pytanie o przekształcenie f(x) i f(|x|)
16 mar 00:29
Tadeusz:
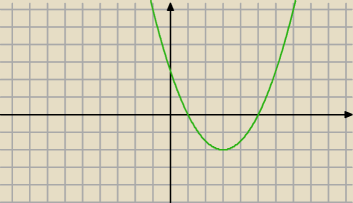
tylko tego typu f(x) po "przekształceniu" w f(|x|) będzie miała 4 pierwiastki
16 mar 00:34
adam: Równanie to ma 4 rozwiązania, gdy:
m<−1
1<m<5/3
16 mar 07:54
Jerzy:
To zadanie rozwiązuje się w trzech linijkach.
Podstawienie: t = |x| i warunek : t > 0
Mamy równanie: t2 + 2(m−3)*t + m2 − 1 = 0 i ma mieć dwa pierwistki dodatnie:
1) Δ > 0
2) t1*t2 > 0
3) t1 + t2 > 0
16 mar 08:26
Jerzy:
| | 5 | |
Rozwiązanie: m ∊ (−∞;−1) U (1; |
| ) |
| | 3 | |
16 mar 08:51