Wykaż, że... nicnieumiem: Punkty K i L są środkami boków odpowiednio AD i CD równoległoboku ABCD. Wykaż, że odcinki BK i BL dzielą przekątną AC na trzy odcinki o równych długościach. Jak to wykazać? Ktoś pomoże?

ElizaR: Jest to klasyczne ( i dobrze znane ) zadanie na kilkukrotne zastosowanie tw. Talesa. Sztuczka polega na przedłużeniu boku AB w lewo oraz boku BC w górę i poprowadzeniu prostej (KL) do przecięcia z prostą (AB) w P oraz z prostą (BC) w Q. Otrzymujemy "motylek" talesowski KDLCQ i "motylek" PAKDL. Z nich to otrzymujemy, że PK=KL=LQ. Ponadto, jako że KL jest linią środkową w ΔACD, mamy KL = 1/2*AC. Z konstrukcji ( i z motylków ) wynika, że PA = 1/2*AB.Rozpatrując układ Talesa dla ΔPKB z fragmentem przekątnej AC ( równoległej do PK), wnosimy, że ów fragment = 2/3*(1/2AC)= 1/3AC Analogicznie potraktujemy fragment przekątnej od strony wierzchołka C...

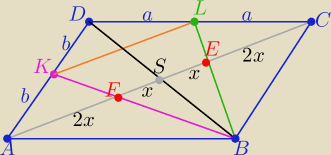
Eta: Można też tak: ( bez Talesa) 1/ ΔABD i BCD są przystające 2/ Przekątne AC i BD dzielą się na połowy 3/ to SC i BL −− środkowe ΔBCD przecinają się w punkcie E i dzielą się w stosunku 2:1 zatem |CE|=|EF|=|AF|= 2x to |AC|=6x Wniosek .... i mamy tezę

nicnieumiem: Dziękuję za pomoc