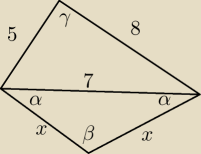
sympatyczne zadanie z kiełbasy maska: Dwa sąsiednie boki czworokąta wpisanego w okrąg mają długości 5 cm i 8 cm, przekątna której końcami są końce tych boków, ma długość 7 cm, a pozostałe dwa boki mają równą długość. Oblicz pole tego czworokąta. β = 180 − 2α = 90 − α Czworokąt wpisany w okrąg więc γ = 90 + α Twierdzenie cosinusów cos(90 + α) = − sin α 7² = 5² +8² + 2*5*8*sinα −40 = 80 * sinα

	1
sinα = −
	2

α = 120 Coś z kątami nie jest tak, pewnie głupi błąd.. albo może i nie, w każdym razie ktoś wyłapał co robię źle?

	109√3
Ps wynik to
	6

'Leszek: Blad masz juz w wyrazeniu : β = 180° − 2α ≠ 90° − α ?

'Leszek: i dalej β + γ = 180° ⇒ γ = 180 ° − β = 180 ° − ( 180° − 2α) = 2α

maska: Czyli z twierdzenia cosinusów mam −1/2 = cos2α α = 60 ?

maska: Coś nie pasuje

maska: A dobrze w ogóle założyłem że tam gdzie są kąty α to są równe kąty?

'Leszek: Nie , z twierdzenia cosinusow dla Δ ( u gory twojego rys. ) cos γ = 1/2 ⇒ γ = 60 ° ⇒ α = 30 °, β = 120° Z tw.cosinusow dla drugiego Δ otrzymasz 7² = 2x²*(1 − cos β) ⇒ x = 7√3/3 Teraz polocz pola trojkatow ze wzoru P = 0,5 a*b*sin δ ( wzor ogolny) Powodzenia !

maska: 7² = 2x²*(1 − cos β) ? A nie

	1
72 = 2x2 + x2 *
	2

?

maska: cosβ = (90 + 30) = − sin 30 = − 1/2

'Leszek: Tw . cosinusow dla dolnego Δ (powinienes na swoim rysunku oznaczyc wierzcholki ) 7² = x² + x² − 2x*x * cos β ⇔ 7² = 2x² *( 1− cos β)⇔ 49 = 2x² * 1,5⇒x= 7/√3

maska: Dzięki za zainteresowanie tematem. Wyciągnę wnioski ze swoich błędów.

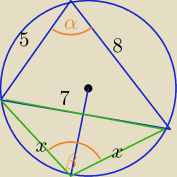
Mila: 7²=5²+8²−2*5*8*cosα

	1
cosα=
	2

α=60^o β=120 7²=x²+x²−2*x*x*cos(120^o)

	1
49=2x2+2*x2*
	2

49=3x²

	7
x=
	√3

	1		1		7		7
P=		*5*8*sin60+		*		*		*sin120
	2		2		√3		√3

	√3		49		√3
P=20*		+		*
	2		6		2

	169√3
P=
	12

'Leszek: P.Mila podala prawidlowy wynik ,ja otrzymalem taki sam wynik na pole czworokata P = 169√3/12

maska: Czyli w książce jest jednak błąd, teżmi tyle wychodzi, ale już nie chciałem zawracać głowy. Szkoda, że w takim zadaniu, bo strasznie mi się spodobało.

adam: U mnie też wyszło: 169/(4√3) czyli (169√3)/12 Tylko że ja zrobiłem to inną metodą: 1) wrzuciłem przekątną 7 na oś OX układu współrzędnych 2) za pomocą dwóch okręgów o r=5, i r=8 wyznaczyłem współrzędne wierzchołka α, 3) za pomocą okręgu opisanego na powstałym trójkącie i symetrycznej boku 7 wyznaczyłem współrzędne wierzchołka β, 4) mając współrzędne czterech wierzchołków czworokąta obliczyłem pole. *) α i β odnoszą się do rysunku Mili.