Pomocy ADA: Czy dacie radę to policzyć. Napiszcie po kolei co z czego wychodziJaki promień ma okrąg opisany na trójkącie równobocznym o boku 2

Janek191:

	2		√3		√3
R =		h h = a		= 2		= √3
	3		2		2

	2
R =		√3
	3

Antonni:

	a
R=
	2sinα

a=2 α= 60^o Mozna ljuz liczyc

'Leszek: W sposob bardziej elementarny : Nalezy wykonac rysunek ,niech O oznacz srodek okregu, znajduje sie w punkcie przeciecia dwusiecznych kata ,zas a − bok Δ AB podstawa , D spodek wysokosci Δ czyli srodek boku AB Wowczas w Δ ADO kat DAO = α = 30° z funkcji trygonometrycznej , oraz AD= a/2 , cos α = 0,5a/R ⇒ R = 0,5a/cos 30° ⇒ R = a√3/3

Eta:

	a√3
R=		=........
	3

BB: Janek 191 z ką wiozłeś √3 w wyrażeniu h= a ...

Janek191: Z głowy wiozłem

BB: Janek 191 jak z głowy

Janek191: Wzory są w głowie

Eta: Zobacz w karcie wzorów ( trójkąt równoboczny

	a√3
tam masz h=
	2

	2		a√3
R=		h= .. =
	3		3

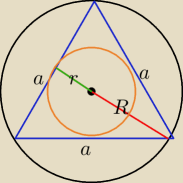
Mila: R=2r h=3r

	a√3
h=		( z tw. Pitagorasa)
	2

	2		2		a√3		a√3
R=		h=		*		=
	3		3		2		3

BB: w rozwiązaniach w książce niema takiego wyniku

'Leszek: A jaka to ksiazka ? ?

Mila: A co masz w książce?

	2√3
R=
	3

Eta: podstaw za a=2

	2√3
Odp:
	3

BB: Mila są takie rozwiążania i jedno z nich jest poprawne √3 , ¹₃√3, ²₃√3 2√3

Janek191: 3)

Mila: no to przecież masz : ! bo :

2√3		2
	=		√3
3		3

BB: dzięki teraz mnie olśniło

Mila: