przyprostokątne bla bla: Przeciwprostokątna trójkąta prostokątnego ma długość 10 cm. Jakie powinny być długości przyprostokątnych tego trójkąta aby kwadrat długości jego wysokości poprowadzonej z wierzchołka kąta prostego miał największą wartość?

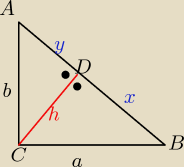
Eta: x+y= 10 => x = 10 −y , dla y€(0,10) h² = x*y −−− ta funkcja ma mieć maximum to h²= f( y) = (10−y)*y= −y² +10y −−− to f, kwadratowa (parabola ramionami do dołu)

	−10
więc osiąga max, dla ymax=		= 5
	2*(−1)

to x_max= 10 −5= 5 czyli h² = 5*5=25 => h= 5 dalej już dokończ sama i wyznacz długości "a" i "b" Miłych snów

bla bla: nie za bardzo rozumiem tylko skąd się wzięło h² = x*y ...

Eta: twierdzenie: długość wysokości poprowadzonej z wierzchołka kąta prostego równa jest średniej geometrycznej długości odcinków na jakie ta wysokość podzieliła przeciwprostokątną . dowód: ΔCBD ~ΔCDA z cechy ( k,b,k)

	h		x
więc		=
	y		h

to h²= x*y co kończy dowód