Rachunek prawdopodobieństwa
Michał: Oblicz P(A ∪ B), jeśli P(A' ∩ B') = 0,3.
15 mar 10:54
Michał:
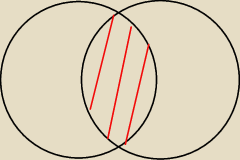
Zaznaczony fragment to P(A' ∩ B') = P(A' ∪ B') = 0,3.
A więc P(A ∪ B) = 0,7. Czy dobrze zrozumiałem to zadanie?
15 mar 11:08
Michał: Kolejne zadanie:
Wykaż, że jeżeli P(A ∩ B) = P(A) * P(B), to P(A' ∩ B') = P(A') * P(B').
15 mar 11:36
Michał: Proszę o pomoc.
15 mar 16:32
Michał: Podbijam.
15 mar 22:15
eight: P(A' ∩ B') = P(A') * P(B').
x e A' n B' <=> x ∉ A u B < = > x ∉A n x∉ B <=> x e A' n x e B', więc P(A') * P(B')
15 mar 22:18
Michał: Dziękuję.
15 mar 22:41
olekturbo: 11:08 zle
P(A'NB') = P(ANB)'
15 mar 22:47
eight: 22:47 źle
15 mar 22:50
eight: P(A'nB') = P(AuB)'
15 mar 22:51
 Zaznaczony fragment to P(A' ∩ B') = P(A' ∪ B') = 0,3.
A więc P(A ∪ B) = 0,7. Czy dobrze zrozumiałem to zadanie?
Zaznaczony fragment to P(A' ∩ B') = P(A' ∪ B') = 0,3.
A więc P(A ∪ B) = 0,7. Czy dobrze zrozumiałem to zadanie?