geometria analityczna
ape: Dany jest trójkąt o wierzchołkach A = (−4, −1), B = (−7, −5), C = (4, −7). Oblicz długość
odcinka AD dwusiecznej kata przy wierzchołku A.
Wiem, że przy wierzchołku A jest kąt prosty. Myślałam żeby z twierdzenia o dwusiecznej obliczyć
na jakie odcinki dwusieczna podzieliła przeciwprostokątną, a potem z twierdzenia cosinusów
obliczyć wymaganą długość, ale zapowiadają się dość nieprzyjemne rachunki. Może jest jakiś
szybszy sposób?
14 mar 22:31
Mila:
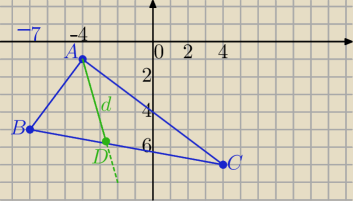
|AB|=
√32+42=5
|AC|=8
2+6
2}=10
|BC|=
√112+22=
√125
(
√125)
2=5
2+10
2− Δjest prostokątny
| | 1 | | 1 | |
PΔABC= |
| *5*d*sin45o+ |
| *10*d*sin45o⇔ |
| | 2 | | 2 | |
| 1 | | √2 | | 1 | | √2 | |
| *5*d* |
| + |
| *10*d* |
| =25 /*4 |
| 2 | | 2 | | 2 | | 2 | |
5d*
√2+10*d
√2=100
15
√2*d=100
14 mar 23:02
Eta:
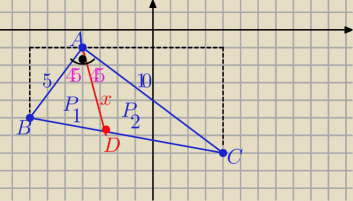
1/ wykaż,że trójkąt ABC jest prostokątny
2/ |AB|=
√42+32=5 , |AC|=
√82+62=10
3/ P(ABC)= 25
| | 1 | | 1 | |
4/ P(ABC)= P1+P2 ⇒ |
| *5*x*sin45o+ |
| *x*10*sin45o=25 |
| | 2 | | 2 | |
wyznacz "x"
x=|AD|=.....
14 mar 23:04
Eta:

14 mar 23:04
ape: Dziękuje Wam serdecznie

15 mar 00:10
adam:
D=(−10/3, −17/3)
|AD|=(10√2)/3
15 mar 08:36
 |AB|=√32+42=5
|AC|=82+62}=10
|BC|=√112+22=√125
(√125)2=52+102− Δjest prostokątny
|AB|=√32+42=5
|AC|=82+62}=10
|BC|=√112+22=√125
(√125)2=52+102− Δjest prostokątny
 1/ wykaż,że trójkąt ABC jest prostokątny
2/ |AB|=√42+32=5 , |AC|=√82+62=10
3/ P(ABC)= 25
1/ wykaż,że trójkąt ABC jest prostokątny
2/ |AB|=√42+32=5 , |AC|=√82+62=10
3/ P(ABC)= 25

