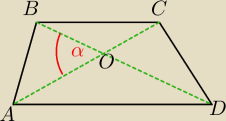
Pole trapezu ABCD o podstawach AD i BC (AD > BC) jest równe 48.
Punkt O jest punktem przecięcia przekątnych trapezu.
Pole trójkąta AOB jest równe 9.
Wyznaczyć stosunek długości AD i BC podstaw trapezu.
Ktoś może ma jakikolwiek pomysł na to zadanie?
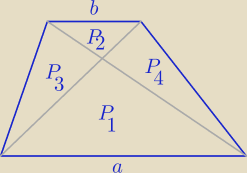P=48 i P1=9
| a | ||
k= | , k>0 | |
| b |
| √P1 | 3 | 4√3+3 | ||||
k= | = | = ...........= | ||||
| √P2 | 4√3−3 | 13 |
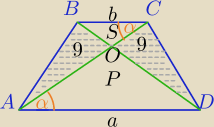b<a
PΔAOB=PΔCOD=9
| b | OC | b | ||||
ΔBOC ∼ΔAOD w skali k= | ⇒ | = | ||||
| a | OA | a |
| 9 | OC | 9 | b | a | |||||
= | ⇔ | = | ⇔P=9* | ||||||
| P | OA | P | a | b |
| S | b | b | |||
=( | )2⇔ S=( | )2*P | |||
| P | a | a |
| b | ||
( | )2*P+P−30=0⇔ | |
| a |
| b | a | |||
9* | +9* | −30=0 | ||
| a | b |
| b | |
=x, x∊(0,1) | |
| a |
| 9 | ||
9x+ | −30=0 | |
| x |
| 1 | ||
x= | posprawdzaj rachunki | |
| 3 |
| b | 1 | ||
= | |||
| a | 3 |