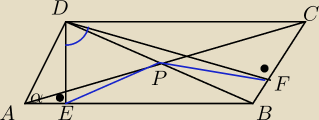
Mam wykazać, że wiedząc o tym, że kąt ostry tego równoległoboku ma miarę α, kąt |∡EPF|=2α.
Dodatkową informacją jest to, że punkt P to jest punktem przecięcia przekątnych AC i BD.
Wcześniej wykazałem, że na czworokącie DEBF można opisać okrąg, oraz to, że |∡EDF|=α.