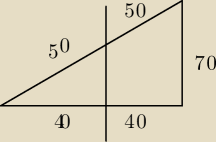
Twierdzenie Talesa Cezary: Trójkątną działkę o bokach 100, 80 i 70 m należy podzielić na dwie działki o równym polu, prowadząc przez działkę linię graniczną równoległą do najdłuższego boku. Oblicz: a) Jaki będzie obwód trójkątnej działki powstałej po podziale; b) Jakie będą długości podstaw drugiej działki (tej o kształcie trapezu) Zupełnie nie mogę sobie tego zobrazować. Wiem że to z Twierdzenia Talesa. Czy rysunek ma wyglądać tak?

Jack: "Rownolegla do najdluzszego boku" czyli do przeciwprostokatnej. A Ty narysowales ze do przyprostokatnej

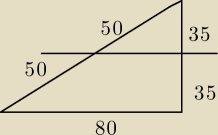
Cezary: aaa ok czyli tak?

Cezary: Nie rozumiem dlaczego obwód w a) ma wyjść

250
√2

Jerzy: Wiesz co to jest równoległa do najdłuższego boku ?

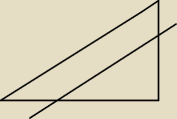
Cezary: Cos takiego?

Jerzy: Dokładnie tak.

adam: Jeśli pole trójkąta zmniejszysz o połowę, to boki trójkąta zmniejszą się o współczynnik k=1/√2 więc obwód wynosi 100k+80k+70k=250k ⇒ 250/√2 A k obliczysz ze wzoru na pole trójkąta: P= 1/4 √(a + b − c) (a − b + c) (−a + b + c) (a + b + c) gdzie dla P/2 a→ak, b→bk, c→ck