Okrąg wpisany w trójkąt
ElizaR: Okrąg wpisany w trójkąt.
Witam, czy ktoś zna ELEMENTARNY ( tj. z wykorzystaniem jedynie aparatu matematycznego obecnej
szkoły średniej) dowód następującego twierdzenia:
«Trójkąt ABC jest wpisany w okrąg o środku O. Niech K, L, M będą środkami łuków AB, BC, CA tego
okręgu ( tj. łuków nie zawierających trzeciego wierzchołka).
Tworzymy sumę wektorową v(OK) + v(OL) + v(OM) = v(OS). Wtedy S jest środkiem okręgu WPISANEGO
w trójkąt ABC.»
13 mar 23:22
ElizaR: ?
14 mar 00:57
ElizaR: ?... Czy są prawdziwi matematycy / uzdolnieni studenci matematyki na tym portalu? Niech się
ujawnią!
14 mar 09:34
ElizaR: ?
14 mar 10:53
ElizaR: Nikt naprawdę nic nie ma do powiedzenia w tej materii?
15 mar 13:18
ElizaR: ?
15 mar 21:45
ElizaR: Myślałam, ze to forum nie jest li−tylko darmową korepetytornią do odrabiania zadań szkolnych.
Myślałam,że znajdą się tu ludzie z matematycznymi zainteresowaniami pozaszkolnymi...
15 mar 22:31
ElizaR: I... −jak na razie− zawiodłam sie!
15 mar 23:17
g:
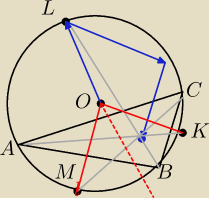
Plan dowodu byłby taki:
1) zauważyć że środek okręgu wpisanego leży na cięciwach AK,BL i CM,
2) pokazać że dwusieczna kąta MOK jest równoległa do dwusiecznej kąta ABC,
3) z 2) wynika że suma wektorów OK+OM poprowadzona z punktu L leży na cięciwie LB,
4) stąd suma wszystkich trzech wektorów leży na LB.
5) analogicznie musi leżeć na AK i CM, wiec jest to środek okręgu wpisanego.
16 mar 00:41
ElizaR: Dzięki za pomysł! Wszystko jest jasne i przejrzyste. Ten fakt, bardzo ładny, nie funkcjonuje w
ogóle w obiegu
szkolnym, ( dlaczego?) natomiast jest często wykorzystywany przy dowodzeniu własności
geometrycznych na płaszczyżnie Gaussa.
Dowód "zespolony" jest banalny; bardzo mnie interesowało, czy względnie nieskomplikowany jest
dowód "klasyczny", a
nie udawało mi się znaleźć "punktu zaczepienia", którym w tym przypadku okazał się punkt 2)
planu dowodu...
Bardzo się cieszę!
16 mar 09:02
g: A jak wygląda dowód zespolony?
16 mar 11:29
 Plan dowodu byłby taki:
1) zauważyć że środek okręgu wpisanego leży na cięciwach AK,BL i CM,
2) pokazać że dwusieczna kąta MOK jest równoległa do dwusiecznej kąta ABC,
3) z 2) wynika że suma wektorów OK+OM poprowadzona z punktu L leży na cięciwie LB,
4) stąd suma wszystkich trzech wektorów leży na LB.
5) analogicznie musi leżeć na AK i CM, wiec jest to środek okręgu wpisanego.
Plan dowodu byłby taki:
1) zauważyć że środek okręgu wpisanego leży na cięciwach AK,BL i CM,
2) pokazać że dwusieczna kąta MOK jest równoległa do dwusiecznej kąta ABC,
3) z 2) wynika że suma wektorów OK+OM poprowadzona z punktu L leży na cięciwie LB,
4) stąd suma wszystkich trzech wektorów leży na LB.
5) analogicznie musi leżeć na AK i CM, wiec jest to środek okręgu wpisanego.