Przebieg zmienności funkcji, monotoniczność i ekstrema. Mimoza: Witam! Zadanie to dotyczy przebiegu zmienności funkcji, a dokładniej momentu w którym utknęłam. y=(1−x)/((x+2) D: x∊R\{−2} Dochodzę do momentu w którym muszę obliczyć 1 pochodną (monotoniczność i ekstrema) y'=(1−x)/(x+2)= −3/(x+2)² i daną pochodną przyrównuję do 0 −3/(x+2)²=0 −3=0 Co to oznacza? Nie ma ekstremów, monotoniczności? W jaki sposób mam to zapisać/wyjaśnić na egzaminie? 2) Co się dzieje jeżeli obliczam pochodną (znowu te monotoniczności i ekstrema), a następnie deltę i wychodzi mi ona ujemna. Jak ma to zapisać, co się dzieje z funkcją? Nie ma konkretnego przykładu, ale spotkałam się już z czymś takim i nie wiedziałam co zrobić .

Tadeusz: toć to funkcja homograficzna ... to że nie ma ekstremów nie znaczy że nie jest monotoniczna

Mimoza: Dziękuję serdecznie za odpowiedź! To wiele wyjaśnia .

Tadeusz:

Jack:

	−3
y' =
	(x+2)2

po przyrownaniu do zera otrzymujemy sprzecznosc (czyt. brak ekstremow) co do monotonicznosc y'>0 funkcja rosnie y'<0 funkcja maleje jednakze mianownik to liczba do kwadratu czyli > 0 zatem skoro licznik jest ujemny, to liczba ujemna podzielona przez dodatnia da liczbe ujemna. wniosek : funkcja malejaca w calej swojej dziedzinie.

Mimoza: Dziękuję Jack teraz już wszystko rozumiem !

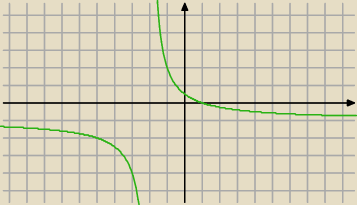
Jack: wlasciwie to moznaby sie troszke poklocic co do malejacej w calej swojej dziedzinie bo jak spojrzymy na wykres z lewej strony minus dwojki, to widzimy ze funkcja idzie w dol, nieskonczenie w dol. Natomiast z prawej strony minus dwojki idzie z gory w dol. To pytanie − jak to moze byc malejaca skoro idzie w dol i nagle jest na gorze ? wiec bezpieczniej jest zapisac dla x ∊ (−∞;−2) funkcja maleje dla x ∊ (−2;∞) funkcja maleje.