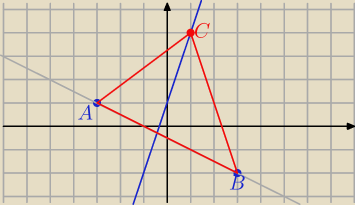
Oblicz współrzędne wierzchołka . Bk: Pole trójkąta ABC o wierzchołkach A(−3,1) i B(3,−2) jest równe 15. Wierzchołek C należy do prostej o równaniu y=3x+1. Oblicz współrzędne wierzchołka C .

Tadeusz: Policz długość odcinka AB Znając pole wyznaczysz wysokość trójkąta opuszczoną z C na AB Jest ona jednocześnie odległością punktu C od prostej przechodzącej przez A i B i to byłoby na tyle

Janek191: C = ( x₀, y₀) = ( x₀, 3 x₀ + 1) I A B I = √6² + 3² = √36 + 9 = √45 = 3√5 P = 0,5*3√5*h = 15 / *2 3√5 h = 30 h = 2√5 oraz prosta AB

	−3
a =		= −0,5
	6

y = − 0,5 x + b A = ( −3 , 1) 1 = −0,5*(−3) + b b = −0,5 y = − 0,5 x − 0,5 / * 2 2 y = − x − 1 x +2 y + 1 = 0 Odległość punktu C od tej prostej h = 2√5, więc

I 1*x0 + 2*(3 x0 + 1) + 1I
	= 2√5 / * √5
√1 + 4

I 7 x₀ + 3 I = 10 7 x₀ + 3 = − 10 lub 7 x₀ + 3 = 10 7 x₀ = − 13 lub 7 x₀ = 7

	13
x0 = −		lub x0 = 1
	7

	39		32
y0 = −		+ 1 = −		lub y0 = 4
	7		7

Odp.

	13		32
C = ( 1, 4) lub C = ( −		, −		)
	7		7

==========================================

Eta: 2 sposób C∊ (y=3x+1) ⇒C(x, 3x+1) → AB=[6,−3] → AC=[x+3, 3x] P= 0,5|6*3x−(−3)*(x+3)]| ⇒ |21x+9|=30 /:3

	13		32
|7x+3|=10 ⇒ 7x+3=10 v 7x+3= −10 ⇒ x=1 v x= −		to y= 3x+1 ⇒ y= 4 v y= −
	7		7

	13		32
C(1,4) , C(−		, −		)
	7		7