Zadanie geometria
KlaudiaK: Na czworokącie wypukłym ABCD opisano okrąg o środku S. Wiedząc, że |AC| = |AB| oraz |DC| = 5,
|AD| = 4, |BD| = 6, oblicz promień okręgu opisanego na czworokącie.
13 mar 14:23
Janek191:
Czy dobrze przepisana jest treść zadania ?
13 mar 14:35
KlaudiaK: Niestety tak
13 mar 14:38
Janek191:
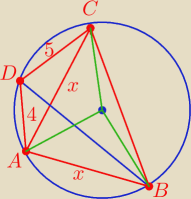
13 mar 14:54
Kacper:

13 mar 15:45
KlaudiaK: Mogę prosić o pomoc?
13 mar 22:00
Marcin : Ktoś coś?
25 sie 19:25
Adamm: 4
2+6
2−2*4*6*cosα=x
2
| | y | |
x2+y2−2*x*y*cosα=x2 ⇒ cosα= |
| |
| | 2x | |
| | x2−9 | |
42+x2−2x*4*cosβ=52 ⇒ |
| =cosβ |
| | 8x | |
6
2+y
2−2*6*y*cosβ=5
2
x
6−68x
4+508x
2+23184=0
t=x
2
t
3−68t
2+508t+23184=0
t=−14 jest rozwiązaniem
| t3−68t2+508t+23184 | |
| =t2−82t+1656=0 |
| t+14 | |
t=46 lub t=36
x=
√46 lub x=6
r
2+r
2−2r*r*cos2α=x
2
cos2α=2cos
2α−1
cosα=1/8 lub cosα=1/3
cos2α=−31/32 lub cos2α=−7/9
r=4
√2898/63 lub r=18
√23/23
teraz pewnie jakaś nierówność trójkąta by wykluczyć jedną z odpowiedzi
25 sie 20:36
Eta:
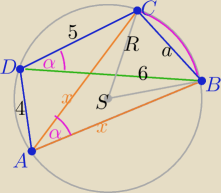
1/ z tw. Ptolemeusza : 6*x=5*x+4*a ⇒ x=4a
2/ z tw. cosinusów w ΔABC :
| | 16a2+16a2−a2 | | 31 | |
cosα= |
| = |
| |
| | 2*4a*4a | | 32 | |
| | 3√7 | |
to sinα= √1−cos2α= ..= |
| |
| | 32 | |
3/ z tw. cosinusów w ΔBDC ( gdzie kąt |BDC|=α ( jako wpisany oparty na łuku BC
| | 31 | | 23 | |
a2=52+62−2*5*6* |
| =............= |
| |
| | 32 | | 8 | |
| | a | |
4/ z tw. sinusów 2R= |
| |
| | sinα | |
| | a | | 4√322 | |
R= |
| =...... R= |
| |
| | 2sinα | | 21 | |
============
25 sie 21:36
Mila:
Wszystko się zgadza, jak w szwajcarskim zegarku< kwiatek>.
25 sie 22:13
Mila:
Już gdzieś rozwiązywałam ta metodą podobne zadanie, ale ta wyszukiwarka słabo działa.
(1) x=4a tw. Ptolemeusza.
(3) a =2R sinα w ΔABC
(4) (2Rsinα)
2=5
2+6
2−2*5*6*cosα w ΔDBC
R= jak wyżej.
25 sie 22:36
Marcin : Dziękuję bardzo za pomoc, zawsze można na Was liczyć


26 sie 12:19


 1/ z tw. Ptolemeusza : 6*x=5*x+4*a ⇒ x=4a
2/ z tw. cosinusów w ΔABC :
1/ z tw. Ptolemeusza : 6*x=5*x+4*a ⇒ x=4a
2/ z tw. cosinusów w ΔABC :

