Geometria analityczna nicnieumiem: Prosta o równaniu y=−2x+3 zawiera jeden z boków kwadratu, a punkt S=(3,12) jest środkiem symetrii tego kwadratu. a) Oblicz pole koła wpisanego w ten kwadrat b) Oblicz pole koła opisanego na tym kwadracie Proszę o ROZWIĄZANIE tego zadania krok po kroku, z góry dziękuję.

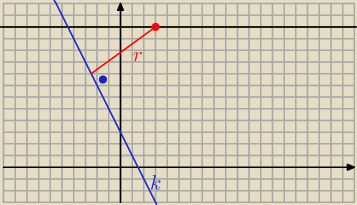
Janek191: a) r = −odległość punktu S od prostej k : y = −2 x + 3

nicnieumiem: Wspaniale. Czy jest na tej stronie ktoś, kto to zadanie faktycznie rozwiąże?

Janek191: a) 2 x + y − 3 = 0 S = (3 ,12)

	I 2*3 + 1*12 − 3 I		15
r =		=
	√22 + 12		√5

więc

	15
Pkw = π*(		)2 = 45π
	√5

nicnieumiem: Naprawdę nic z tego nie ogarniam. Nie wiem, skąd wziął się ten wzór na r. Już od godziny próbuję to zadanie rozwiązać, ale najwyraźniej muszę je sobie odpuścić.

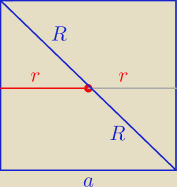
Janek191: b)

	15
R = r √2 =		*√2 = 3√10
	√5

P_ko = π R² = π * ( 3 √10)² = π* 9*10 = 90π

Janek191: Równanie prostej A x + B y + C = 0 P = ( x₀, y₀) d − odległość punktu P od tej prostej:

	I A*x0 + B* y0 + C I
d =
	√A2 + B2

My mamy prostą 2 x + y − 3 = 0 P = S = ( 3, 12) więc A = 2 B = 1 C = − 3 Wstawiamy do wzoru

	I 2*3 + 1*12 − 3 I
r = d =		=
	√22 + 12

nicnieumiem: Bardzo dziękuję, właśnie o to mi chodziło. Teraz wszystko jest już jasne