Pochodne confusing: Dana jest funkcja x³−6x²+7x+2. Wyznacz równani jest stycznej do wykresu funkcji, która ma najmniejszy współczynnik kierunkowy i która przechodzi przez punkt A=(1,4). Obliczyłam, ale cos mi źle wychodzi, bo tylko w sumie jeden współczynnik kierunkowy mi wychodzi. A skoro podali, ze trzeba wybrac, więc pewnie źle rozwiązałam. Na poczatku wyliczyłam pochodna, a póxniej styczną do niej, gdzie pod x0 wpisałam 4

Adamm: f(x)=x³−6x²+7x+2 f'(x)=3x²−12x+7 y=f'(x₀)(x−x₀)+f(x₀) 4=f'(x₀)(1−x₀)+f(x₀) 4=(3x₀²−12x₀+7)(1−x₀)+x₀³−6x₀²+7x₀+2 x₀=1 lub x₀=5/2 najmniejszy współczynnik mamy dla x₀=5/2

Tadeusz: czyżby?

confusing: Ok, czyli źle zrobiłam w momencie, gdy podstawiłam 4 pod x0, a nie pod x, Dziękuję

Tadeusz: tyle, że Adamm nie zrobił tego dobrze

confusing: Tzn. sposób chyba dobry, ale x0 źle wyznaczył. Muszę zaraz Hornerem spróbować. W tym jest błąd?

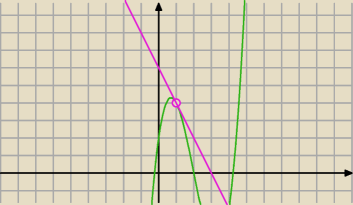
Tadeusz: i współczynnik −2 Druga styczna styczna przechodząca przez ten punkt ma współczynnik dodatni

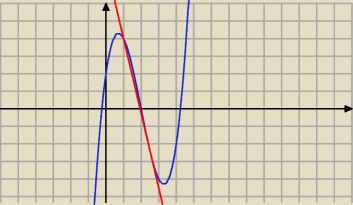
Adamm: druga styczna wcale nie ma współczynnika dodatniego

confusing: Czyli, jak obliczę ro równanie, które wyszło Adamowi: 4=(3x02−12x0+7)(1−x0)+x03−6x02+7x0+2. Powstanie: 0=−2x₀⁴+9x₀²−12x₀+9 I to równanie stycznej? A współczynnikiem kierunkowym jest własnie to −2?

Tadeusz: druga styczna ma współczynnik też ujemny ... masz rację Adamm a na dodatek najmniejszy bo równy −4,25