Z Opos: Oblicz pole obszaru ograniczonego łukami paraboli y²=2x i okręgu x²+y²−4x=0. Proszę o wyjaśnienie tego zadania, jak powinno się je rozwiązać za pomocą całek oznaczonych.

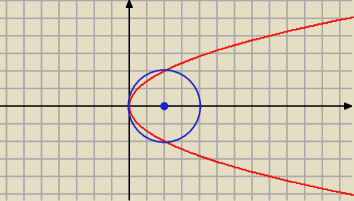
Janek191: (x − 2)² − 4 + y² = 0 ( x − 2)² + y² = 2² 2 P = 2 ∫ [√ 4 −(x −2)² − √2x] dx = 0

Opos:

	1
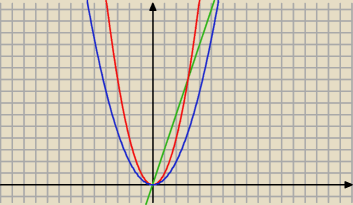
Dzięki wielkie, a jak będzie z obszarem wspólnym 2 parabol i prostej ? tj. y=x2, y=		x2,
	2

y=3x. Oblicz pole wspólnego obszaru ograniczonego tymi krzywymi.

Opos:

Janek191:

Janek191: Znajdź punkty wspólne krzywych z prostą.

Opos: x=0 i x=3 oraz x=6

Opos: Tylko nie wiem jak ująć to w całkę.

Janek191: 3 6 6 P = ∫ x² dx + 3 ∫ x dx − 0,5 ∫ x² dx = 0 3 0

Opos: Dziękuję bardzo