Pomoże ktoś z tym zadankiem tak od ,,a" do ,,z"??? Ania: W trójkącie ostrokątnym |𝐴𝐵| = 2, |𝐵𝐶| = 1, sin∠𝐵𝐶𝐴 =2√2/3. Oblicz |𝐴𝐶|.

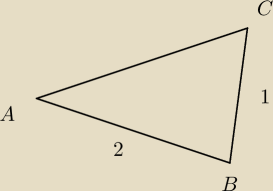
Adamm: oblicz cos∡ABC i z tw. Cosinusów wylicz |AC| (masz sin∡ACB oraz sin∡CAB z tw. Sinusów, policz z tego cos∡ABC)

Ania: nie wiem jak to się liczy bo nigdy tego nie liczyłam

Adamm: biedne dziecko

Ania: wyszło że x² = cos alfa ale nie wiem co za cos podstawić bo tam mam sinus

Ania: podpowiesz?

Adamm: cos∡ABC=cos(180^o−(∡CAB+∡ACB))=−cos(∡CAB+∡ACB)= =sin(∡CAB)*sin(∡ACB)−cos(∡CAB)*cos(∡ACB) liczysz jak powiedziałem cosinusy z jedynki trygonometrycznej (sin²x+cos²x=1) dla kątów ostrych cosinusy są dodatnie więc można opuścić kwadrat ze znakiem + i mamy cosx=√1−sin²x