trapez 123a: przekątne trapezu ABCD w którym AB || CD przecinają się w punkcie P w ten sposób, że |AP| = 9 |CP|=3 |DP|=2 |BP|=6 oraz kąt APB=150. Ile wynosi pole trapezu?

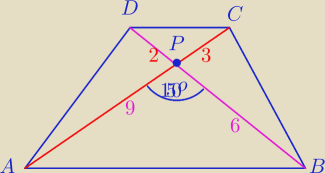
Janek191: Skorzystaj z wzoru na pole Δ: P = 0,5 a*b*sin α

Eta: P=24

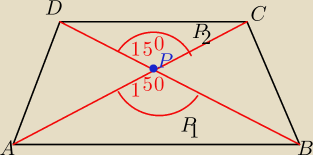
Antonni: P= (√P₁+√P₂)² gdzie P₁ −pole trojkata APB P₂ pole trojkata DPC

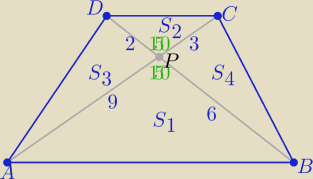
Eta: ΔABP∼ΔDPC w skali k=3

	1		3
S2=		*2*3*sin150o=
	2		2

P(Trapezu)= (k+1)²*S₂

	3
P=16*		= 24
	2

Mila: Wszystkie trapezy dla Ety