Stereometria Matol: Hej Mamy dany czworościan, który ma dwie krawędzie skośne o długości a oraz pozostałe cztery krawędzie o długości b. Oblicz V tego czworościanu. Chcę to zrobic, umieszczając czworościan w graniastosłupie i odejmując od jego V objętości trzech ostrosłupów, które nie są częścią danego czworościanu, ale w połączeniu z nim tworzą graniastosłup. Tyle tylko, że mi nie za bardzo to wychodzi. Help

SEKS INSTRUKTOR : Narysuj proszę ten czworościan, bo coś chyba źle interpretujesz to zadanie.

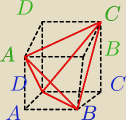
Matol: Czerwony to czworościan, przerywana to ten graniastosłup, a skośne krawędzie to np. BD niebieskie i AC zielone

Matol: *skośne krawędzie o długości a, bo pozostałe też są skończe parami,ale mają długosc b

Matol: **skośne nie skoczne >.<

Adamm:

	5
V=		√b2−a2/2*a2
	12

czy taka jest odpowiedź?

Adamm:

	1
V=		√b2−a2/2*a2 ?
	6

Matol: Niestety nie wiem jaka jest odpowiedź, zadanie podane przez nauczyciela jako praca domowa z jego własnego zbioru

Adamm: nie wiem czy takie wpisanie w graniastosłup jest możliwe ale jeśli tak jest to podstawa jest kwadratem więc bok podstawy to a/√2 stąd h=√b²−a²/2

	1
cała objętość to (a/√2)2*h=		a2*h
	2

	1		1
odejmując cztery równe czworościany o objętościach		*		(a/√2)2*h
	3		2

dostajemy to co podałem ale nie wiem czy to jest ok

Matol: Wydaje się ok, zobaczę jeszcze na lekcji w poniedziałek. Mam jeszcze drugi podpunkt do tego zadania. Jest to sytuacja kiedy każda para krawędzi skośnych w czworościanie ma różną długosc, odpowiednio x,y,z. Jak by to wtedy szło, gdyby też włożyc taki czworościan w graniastosłup. Pytam o ten graniastosłup, bo nauczyciel powiedział, że to jest najlepsza i jedyna metoda na takie zadanie, gdzie krawędzie czworościanu nie są jednakowej długości, ale właśnie są różne patrząc na pary krawędzi skośnych.

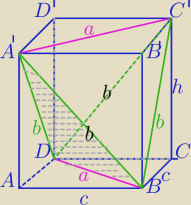
Mila: Po odcięciu 4 naroży otrzymamy czworościan spełniający war. zadania.

	1		1		1
Vcz.=c2*h−4*		*(		c2*h)=		c2*h
	3		2		3

	a
a=c√2⇔c=
	√2

	a2
b2=c2+h2⇔h2=b2−
	2

h=√b²−^a2₂

	1		a
Vcz.=		*(		)2*√b2−a22
	3		√2

	a2√4b2−2a2
Vcz.=
	12

Mila:

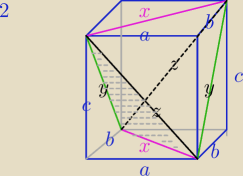
Matol: Dzieki za doprecyzowanie Mila W drugim podpunkcie z pitagorasa jak policzylem mamy x²=a²+b²; z²=a²+c²; y²=b²+c². Z tego wyszły a=√z²+x²−y²/2 ; b=√x²+y²−z²/2 ; c=√z²+y²−x²/2 ~~ calosc pod pierwiastkiem jest podzielona przez 2 A z tego Vcz.=abc − 4*1/3*1/2*abc= 1/3*abc. Brzydkie, ale chyba tak powinno być?

Mila: Wygląda dobrze.( wczoraj rozwiązywałam z innymi oznaczeniami). Widzę, że myślący z Ciebie maturzysta

Mila: Jeśli tak samo postąpisz z wpisaniem czworościanu w sześcian, to masz ułatwione obliczenia dotyczące czworościanu foremnego. ( w tym obliczenie odległości krawędzi skośnych).

Matol: Heh niestety czas leci nieubłaganie i maturka faktycznie za pasem. Od czworoscianu foremnego w szescianie właśnie zaczęliśmy na lekcji, a do domu poszły trudniejsze podpunkty, także dziękuję bardzo za pomoc i miłe słowa Pozdrowionka

Mila: