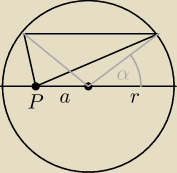
.,., Pełcio: Witam! Poszukuję fajnych rozwiązań tego zadania. Ja znam takie z Pitagorasami, ale może ktoś zna/ widzi inne? Dany jest okrąg o promieniu r. W okręgu tym poprowadzono średnicę i równoległą do niej cięciwę. Na średnicy tej obrano w odległości a od środka okręgu punkt P. Oblicz sumę kwadratów odległości punktu P od końców poprowadzonej cięciwy.

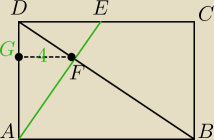
Mila: Dla Pełcia W prostokącie ABCD , w którym |BC | = 8 połączono wierzchołek A z punktem E leżącym na boku DC . Odcinek ten przeciął przekątną BD w punkcie F. Wiedząc, że odległość punktu F od boku AD jest równa 4, oraz że |AE | = 10 oblicz długość boku AB prostokąta.

g: [(r*cosα+a)² + (r*sinα)²] + [(r*cosα−a)² + (r*sinα)²]

Pełcio: g chyba nie rozumiem Jak tu się wgl podpisuje wierzchołki, zawsze rysuję wierzchołki bo jestem ślepy i nie widzę gdzie to jest, haha

Pełcio: literki wierzchołków*

Adamm: jak klikasz rysuję, to tam masz wielką literę T

Mila: Pełcio 1) Dlaczego uznałeś, że ΔABE jest prostokątny? 2) |DE|=6 − dobrze 3) zauważ, że czworokąt ABED jest trapezem. ponadto ΔGFA∼ΔDEA

Pełcio: Dzięki Adamm, cenna informacja

Pełcio: 1) ojoj, dobre pytanie... akurat kompletnie sobie nie uświadomiłem, że to wzór dla prostokątnego, ale ładny blef mi wyszedł myślę dalej

Pełcio: Chyba muszę już teraz dać sobie spokój... mam tak:

6		4
	=
10		10−x

	1
x=3
	3

i mam:

	2
DG= 2
	3

	1
GA= 5
	3

ale i tak nie wiem jak policzyć AB

Mila: Oblicz AF i FE, ustal skalę podobieństwa ΔABF i ΔDEF i dalej pójdzie gładko.

Mila: Dobranoc

Pełcio: Ano właśnie... Dziękuję i dobranoc

tyokke: |AB| = 12?

Pełcio: Tak

Mila: tyokke tak.