Ktoś wie jak rozwiązać to zadanko? Krystian: Wykaż, że środku boków dowolnego czworokąta wypukłego ABCD są wierzchołkami równoległoboku, a jego obwód jest równy sumie długości przekątnych czworokąta ABCD.

Antonni: Do wykazania ze sa wierzcholkami rownolegloboku wykorzystaj tw. o linii srodkowej trojkata

Tadeusz: zrób rysunek. Zauważysz, że boki powstałego czworokąta są parami równoległe do przekątnych.a ich długości to połowa przekątnej

Krystian: i co dalej?

Tadeusz: rysunku jakoś nie widzę

Krystian: bo nie rozumiem treści zadania i nie wiem jak on ma wyglądać

Krystian: ten równoległobok ma być wpisany w ten czworokąt wypukły

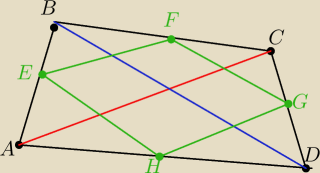
Antonni: Z tw o linii srodkowej trojkata

	1
W ΔABC masz EF=		AC
	2

	1
W ΔACD masz HG=		AC
	2

z tego wynika ze EF= HG Z tego samego tw wynika ze EFIIHG Tak samo rozpatrz teraz ΔABD i ΔBDC i wyciagniuj odpowiednie wnioski

Antonni: Oczywiscie EFGH to jest rownoleglobok