Geometria Analityczna/Planimetria tyokke: Czworokąt wpisany w okrąg. Dwa jego sąsiednie punkty to A=(30;32) i B=(0;8) prosta y=x+2 jest jedyną symetrią tego odcinka i zawiera przekątną AC, oblicz współrzędne C i D. Współrzędną D jestem w stanie policzyć poprzez odległość od prostej y=x+2 która musi być taka sama jak odległość punktu B od prostej y=x+2, ale punktu C kompletnie nie wiem jak policzyć, bo nie wiem jak wykorzystać to że czworokąt jest wpisany w okrąg. Pomocy!

Antonni: Chyba trza warunek wpisania czworokata w okrag wykorzystac

Mila: A skądże masz takie zadanie? Jakieś pokrętne sformułowanie. Może przepisz dokładnie z książki. Odcinek ma dwie osie symetrii.

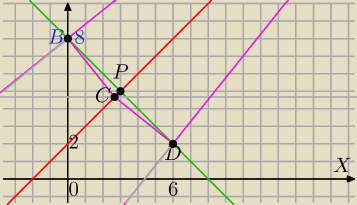
Mila: A=(30,32) B=(0,8) 1) Prosta k: y=x+2 przechodzi przez punkt A i jest osią symetrii czworokąta (tak?) x−y+2=0 2) D leży na prostej AD 3) Odległość Punktu B od prostej k

	|0−8+2		6√2
d(B,k)=		=		=3√2
	√2		2

4) prosta BD⊥k: y=−x+8 5) punkt przecięcia z prostą k x+2=−x+8

	0+xd		8+yd
P=(3,5) to środek odcinka BD , 3=		, 5=
	2		2

D=(6,2) 6) A,B,D należą do okręgu opisanego na danym czworokącie 7) środek okręgu opisanego na czworokącie leży na przecięciu symetralnych boków Napisz wzory symetralnych AB i AD

	4
a) prosta AB: y=		x+8 ,
	5

symetralna AB: S_AB=(15,20)

	5
sab: y=−		x+38.75
	4

	5
b) prosta AD: y=		(x−6)+2
	4

Symetralna:

	4
y=−		x+b , środek AD: SAD=(18,17)
	5

y=−0.8x+31.4 8) Środek okręgu:

	5
y=−0.8x+31.4 i y=−		x+38.75
	4

	1		1
x=16		i y=18
	3		3

	1		1
Q(16		,18		) ∊k
	3		3

W takim razie Q jest środkiem AC

	1		xc+30		1		yc+32
16		=		i 18		=
	3		2		3		2

C=(2²₃,4²₃) ==============