;CCC cynamonek: Dwa kolejne wierzchołki kwadratu mają współrzędne A = (3, −7) B = (−1.−2 ) wyznacz pozostałe wierzchołki Wybaczcie ale jakoś myślę, tak prostego zadania nie moge p

Jerzy: 1) prosta AB 2) odległość AB 3) prostopadłe do AB przez punkty A i B 4) okrąg o środku w A i promieniu IABI 5) punkty przecięcia z prostopadłą przez punkt A 6) okrąg o środku w B i promieniu IABI 7) punkty przecięcia z prostopadłą przez punkt B Wyjdą dwa kwadraty.

Jerzy: Możesz też wykorzystać rachunek wektorowy.

cynamonek: o rachunku wektorowym to jeszcze nie slyszałem ; )

Jerzy: Wykorzystuje się warunek prostopadłości wektorów.

cynamonek: poczytam i się do edukuję : )

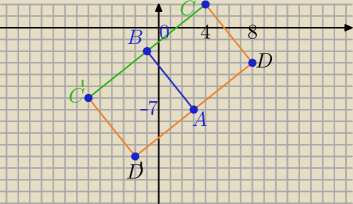
Mila: II sposób (wektory) A = (3, −7) ,B = (−1,−2 ) AB^→=[−4, 5] BC^→⊥AB^→⇔ BC^→=[5,4] lub BC^→=[−5,−4] B(−1,−2)→T_[5,4]→C=(−1+5,−2+4)=(4,2) lub B(−1,−2)→T_[−5,−4]→C'=(−1−5,−2−4)=(−6,−6) −−−−−−−−−−−−−−−−−−−−−−−−−−−− A(3,−7)→T_[5,4]→D=(3+5,−7+4=(8,−3) A(3,−7)→T_[−5,−4]→D=(3−5,−7−4=(−2,−11)

cynamonek: Mila jak coś zrobisz to zawsze tak ładnie, zrozumiale i czytelnie

Antonni: No bo widzisz cynamonku Pani Mila ma wiadomosci ktorych my nie mamy wiec musimy sie duzo jeszcze uczyc.

cynamonek: ehh lubię jak ktoś przykładowo rozwiążę moje zadanie

Antonni: A na maturze kto za Ciebie rozwiaze ? Chyba ze przez

cynamonek: haha Noo ba zrobimy konferencje z Milą ej ale dowiedziałem się ,że wektorowo tego nie mogę robić :C muszę tej 1 słabej metody się uczyć ;>

Jerzy: A czemu uważasz,że jest ona słaba ?

cynamonek: Jakoś tak mi niestety nie leży ale Jak się czegoś nie lubi to trzeba to polubić i tyle

Mila: cynamonek, to pisz wyniki do każdego punktu z wpisu Jerzego z 14:35.

Mila: Oj, chyba utworzę anagram nicka.

Alky: cynamonek, warto jednak ogarnąć sobie rozwiązanie zadań tego typu metodą Mili−wektorowo, bo zajmuje zdecydowanie mniej czasu i mniejsza szansa na pomyłkę Zresztą jak już sobie ogarniesz to wydaje mi się też prostsza ( choć ja jak zaczynałem geometrie analityczną i wpadłem na to zadanie to początkowo robiłem sobie tak na logikę "swoim" sposobem, a więc na piechotkę, tak jak podawał Jerzy na początku, a potem dopiero zauważyłem jak można sobie ułatwić życie przy tego typu zadaniach

Lubięliczyć: Ej, to co na maturze sie tu spotykamy z Milą? Bo ja też 98

Antonni: No ja tez ...8 tak ze bedzie razniej

Alky: Jak ładnie poprosisz to może jeszcze przesiedzi obok 5 lat studiów

Lubięliczyć: Haha, a jak próbne?