Wyznacz maksymalne przedziały monotoniczności Kamil: Wyznacz maksymalne przedziały monotoniczności: f(x) = (x²+3x+1)/(x+3)

Kamil: Obliczyłem pochodną: f'(x) = (x²+6x+8)/(x+3)² = (x+2)(x+4)/(x+3)²

Michał: https://matematykaszkolna.pl/strona/381.html

Janek191:

	(2 x + 3)*(x + 3) − (x2 + 3 x + 1)		x2 + 6 x +8
f '(x) =		=		=
	( x + 3)2		(x + 3)2

	( x + 4)*(x + 2)
=
	(x + 3)2

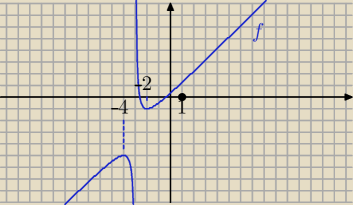
więc f '(x) > 0 dla x ∊ ( − ∞, − 4) ∪ ( − 2, + ∞) − wtedy f rośnie f '(x) < 0 f maleje w ( − 4, − 3) oraz f maleje w ( − 3, − 2) Patrz też na wykres.

Janek191: Mianownik jest > 0 dla x ≠ − 3, więc o znaku pochodnej decyduje ( x + 4)*(x + 2)

Kamil: Dzięki za pomoc... ogarniam już