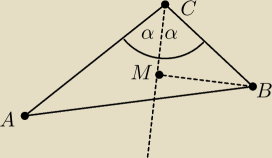
 Dany jest trójkąt ABC o polu równym 1. Z wierzchołka B opuszczamy prostopadły odcinek
BM na dwusieczną kąta C. Oblicz pole trójkąta AMC.
Rozwiązanie od autora:
Pamc=1/2*|AC|*|CM|*sin(α)
|CM| = cos(α)
Pamc = 1/2*|AC|*|CB|*sin(α)*cos(α) = 1/4 * |AC|*|CB|*sin(α) = 1/2* Pabc = 0.5
Jest ktoś w stanie wytłumaczyć skąd wzięła się druga i trzecia linijka rozwiązania?
Dany jest trójkąt ABC o polu równym 1. Z wierzchołka B opuszczamy prostopadły odcinek
BM na dwusieczną kąta C. Oblicz pole trójkąta AMC.
Rozwiązanie od autora:
Pamc=1/2*|AC|*|CM|*sin(α)
|CM| = cos(α)
Pamc = 1/2*|AC|*|CB|*sin(α)*cos(α) = 1/4 * |AC|*|CB|*sin(α) = 1/2* Pabc = 0.5
Jest ktoś w stanie wytłumaczyć skąd wzięła się druga i trzecia linijka rozwiązania?
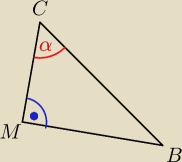 Druga linijka (masz blad, powinno byc tak) :
Druga linijka (masz blad, powinno byc tak) :
| |CM| | ||
cos α = | ||
| |CB| |
| 1 | ||
PAMC = | * |AC| * |CB| * sinα * cosα | |
| 2 |
| 1 | ||
korzystamy z tego, ze sin(2α) = 2sinαcosα zatem | *sin(2α) = sinα*cosα | |
| 2 |
| 1 | 1 | 1 | ||||
... = | * |AC| * |CB| * | * sin(2α) = | * |AC| * |CB| * sin(2α) | |||
| 2 | 2 | 4 |
| 1 | ||
P = | * |AC| * |CB| * sin(2α) = 1 | |
| 2 |
| 1 | 1 | 1 | 1 | 1 | |||||
* |AC| * |CB| * sin(2α)= | * ( | * |AC| * |CB| * sin(2α))= | * 1= | ||||||
| 4 | 2 | 2 | 2 | 2 |
